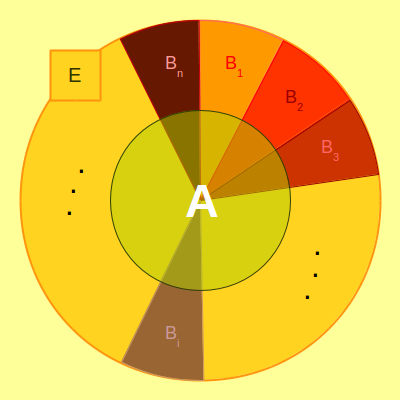
Definíció: Az \(E\) eseménytér \(B_1\), \(B_2\), ..., \(B_n\) részhalmazainak rendszerét teljes esményrendszernek nevezzük, ha:

(1) A \(B_i\) események diszjunktak, azaz\[B_i\cap B_j=\emptyset\text{, ha }i\ne j\]

(2) A \(B_i\) események lefedik \(E\)-t:\[\bigcup_{k=1}^n B_k = B_1\cup B_2\cup\ldots\cup B_n = E\]

A teljes valószínûség tétele

Legyen \(A\subset E\) egy tetszõleges esemény, \(B_1\), \(B_2\), ..., \(B_n\) egy teljes eseményrendszer!

Állítás:
\[
P(A) = P(A\text{ }|\text{ }B_1)\cdot P(B_1) + P(A\text{ }|\text{ }B_2)\cdot P(B_2) + \ldots + P(A\text{ }|\text{ }B_n)\cdot P(B_n) = \sum_{i=1}^n P(A\text{ }|\text{ }B_i)\cdot P(B_i)
\]

Bizonyítás

Tekintsük elöször a tételben szereplõ összeg egy tagját: \[P(A\text{ }|\text{ }B_i)\cdot P(B_i) = \frac{P(A\cap B_i)}{P(B_i)}\cdot P(B_i) = P(A\cap B_i)\] A \(A\cap B_i\) halmazok diszjunktak, hisz' \(B_i\)-k is azok, uniójuk pedig kiadja az \(A\)-t. (Hiszen \(E\) minden eleme, és így \(A\) minden eleme is valamelyik \(B_i\)-nek eleme.) Halmazok diszjunk uniójának valószínûsége a vszg.-ek összege: \begin{equation} \begin{split} P(A) &= P(A\cap B_1)+\ldots+P(A\cap B_n) =\\\\ &= P(A\text{ }|\text{ }B_1)\cdot P(B_1) +\ldots+P(A\text{ }|\text{ }B_n)\cdot P(B_n) \end{split} \end{equation} És ezt akartuk igazolni.