
1. A párhuzamos szelõk tétele
Tétel (a párhuzamos
szelõk tétele): Tekintsünk a síkon egy e, f
metszõ egyenespárt, melyet négy párhuzamos egyenes metsz: a, b, c
és d. (c ≠ d.) A párhuzamosoknak az e-n,
illetve f-en keletkezõ mestzéspontjait jelölje rendre A1,
B1, C1, D1,
illetve A2, B2, C2,
D2.
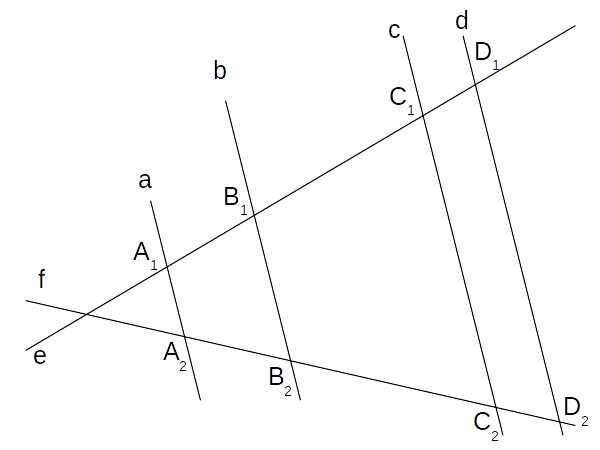
Állítás:\[\frac{A_1B_1}{C_1D_1}=\frac{A_2B_2}{C_2D_2}\](Az
egyik egyenesen fekvõ metszetek aránya megegyezik a másik egyenesen lévõ
megfelelõ metszetek arányával.)

Bizonyítás: (eltûnik)
↑ (megjelenik)
↓
1. eset: Ha
\(A_1B_1=C_1D_1\) (Kattintás az ábrán!),
azaz:
\[\frac{A_1B_1}{C_1D_1}=1\]
(6) Összefoglalva a (3), (4) és (5) alatti eredményeket:
\[A_2B_2 \stackrel{\textrm{(4)}}{=} A_1X \stackrel{\textrm{(3)}}{=} C_1Y \stackrel{\textrm{(5)}}{=} C_2D_2\]És ezt kellett igazolnunk.
2. eset: Az \(\frac{A_1B_1}{C_1D_1}\) arány racionális, vagyis:
\[\frac{A_1B_1}{C_1D_1}=\frac{p}{q}\text{ , ahol }p,q\in\mathbb N^+\]
(4) Így keletkezik az alsó szögszáron az \(A_2B_2\) p részre, ill. a \(C_2D_2\) q részre történõ felosztása. (Katt.)
Ezek egymást közt mind egyenlõk, hisz' a bizonyítás 1. esete épp' azt mondja, hogy ha fent a darabok egyenlõk, akkor lent is.
Eszerint \(A_2B_2\) p-ed része egyenlõ \(C_2D_2\) q-ad részével, amit egy kicsit rendezve:
\begin{equation}
\begin{split}
\frac{A_2B_2}{p} &= \frac{C_2D_2}{q}\\\\
A_2B_2\cdot q &= C_2D_2\cdot p\\\\
\frac{A_2B_2}{C_2D_2} &= \frac{p}{q}
\end{split}
\end{equation}Vagyis ugyanannyi, mint \(\frac{A_1B_1}{C_1D_1}\). Ezzel a 2. eset állítását igazoltuk.
\[\frac{A_1B_1}{C_1D_1}=1\]
| (Azt kell igazolnunk, hogy akkor
\(A_2B_2=C_2D_2\) is igaz.) (1) Húzzunk párhuzamost az A2D2 egyenessel az A1-en ill. a C1-en át! (Kattintás.) A b-n ill. d-n kialakult metszéspontokat jelölje rendre X, ill. Y. (2) A1B1X Δ ≌ C1D1Y Δ (katt.), mert egy oldal és a rajta fekvõ két szög rendre megyegyezik. (Az azonosan jelölt szögek rendre egyállásúak.) (3) Ez alapján: A1X = C1Y (katt.) (4) A1XB2A2 négyszög (katt.) paralelogramma, mert szemközti oldalai párhuzamosak. Így egyenlõk is: A2B2 = A1X. (kattintás) (5) C1YD2C2 négyszög (katt.) is paralelogramma, mert szemközti oldalai párhuzamosak. Így egyenlõk is: C2D2 = C1Y. (kattintás) |

|
(6) Összefoglalva a (3), (4) és (5) alatti eredményeket:
\[A_2B_2 \stackrel{\textrm{(4)}}{=} A_1X \stackrel{\textrm{(3)}}{=} C_1Y \stackrel{\textrm{(5)}}{=} C_2D_2\]És ezt kellett igazolnunk.
2. eset: Az \(\frac{A_1B_1}{C_1D_1}\) arány racionális, vagyis:
\[\frac{A_1B_1}{C_1D_1}=\frac{p}{q}\text{ , ahol }p,q\in\mathbb N^+\]
 |
(1) Az eset feltételét kicsit
átrendezve: \begin{equation} \begin{split} \frac{A_1B_1}{C_1D_1} &= \frac{p}{q}\\\\ A_1B_1\cdot q &= C_1D_1\cdot p\\\\ \frac{A_1B_1}{p} &= \frac{C_1D_1}{q} \end{split} \end{equation}Tehát a feltétel pontosan azt jelenti, hogy \(A_1B_1\) p-ed rész egyenlõ \(C_1D_1\) q-ad részével. (2) Osszuk fel \(A_1B_1\)-et p db, \(C_1D_1\)-et q db egyenlõ részre! (Kattintás.) Ez az összesen p + q db felosztás egymás közt mind egyenlõ. (Az (1) szerint.) (3) Húzzunk párhuzamosakat az osztópontokon át az eredeti (a, b, c, d ) szelõkkel! (Kattintás.) |
(4) Így keletkezik az alsó szögszáron az \(A_2B_2\) p részre, ill. a \(C_2D_2\) q részre történõ felosztása. (Katt.)
Ezek egymást közt mind egyenlõk, hisz' a bizonyítás 1. esete épp' azt mondja, hogy ha fent a darabok egyenlõk, akkor lent is.
Eszerint \(A_2B_2\) p-ed része egyenlõ \(C_2D_2\) q-ad részével, amit egy kicsit rendezve:
\begin{equation}
\begin{split}
\frac{A_2B_2}{p} &= \frac{C_2D_2}{q}\\\\
A_2B_2\cdot q &= C_2D_2\cdot p\\\\
\frac{A_2B_2}{C_2D_2} &= \frac{p}{q}
\end{split}
\end{equation}Vagyis ugyanannyi, mint \(\frac{A_1B_1}{C_1D_1}\). Ezzel a 2. eset állítását igazoltuk.