3. A párhuzamos szelõk tételének megfordítása

A párhuzamos szelõk tétele valami olyasmit állít, hogy ha a szelõk párhuzamosak, akkor az arányok egyenlõk. A párhuzamos szelõk tételének megfordítása azt szeretné igazolni, hogy ha az arányok egyenlõk, akkor szelõk párhuzamosak.

Ez a teljes pompájában álló párhuzamos szelõ-tételre, tehát négy egyenesre nem igazolható, nem igaz.

Igaz azonban a szerényebb verzióra. Ott az állítás megfordítható.

A párhuzamos szelõk tételének megfordítása. Legyenek e és f metszõ egyenesek, melyeket metszenek az a és b egyenesek úgy, hogy\[\frac{A_1M}{B_1M} = \frac{A_2M}{B_2M}\text{, ld. ábra!}\]
ábra
Állítás: Ekkor a szelõk párhuzamosak: a || b.

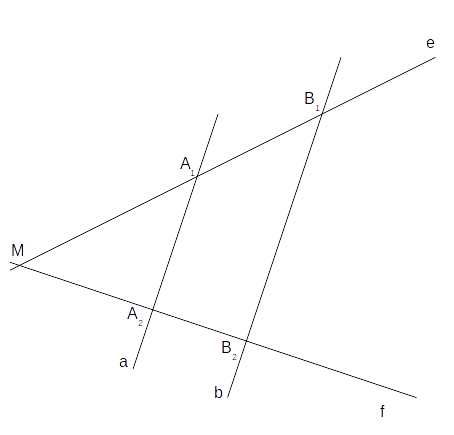
Bizonyítás: (megjelenik) ↓ (eltûnik) ↑

(1) Húzzunk egy x párhuzamost a-val B1-en át! (Kattinatás.) Az x metszéspontját f-fel jelölje X.

(2) Alkalmazzuk a párhuzamos szelõk tételét az a, x szelõkre:\[\frac{A_1M}{B_1M} = \frac{A_2M}{XM}\]
(3) Ebbõl XM-et kifejezve:
\begin{equation}
\begin{split}
\frac{B_1M}{A_1M} &= \frac{XM}{A_2M}\\\\
\frac{A_2M\cdot B_1M}{A_1M} &= XM
\end{split}
\end{equation}
(4) Térjünk most át az állítás feltételére, és abból fejezzük ki B2M-et:
\begin{equation}
\begin{split}
\frac{A_1M}{B_1M} &= \frac{A_2M}{B_2M}\\\\
\frac{B_1M}{A_1M} &= \frac{B_2M}{A_2M}\\\\
\frac{A_2M\cdot B_1M}{A_1M} &= B_2M
\end{split}
\end{equation}
(5) Ennek megfelõen a B2X távolság:
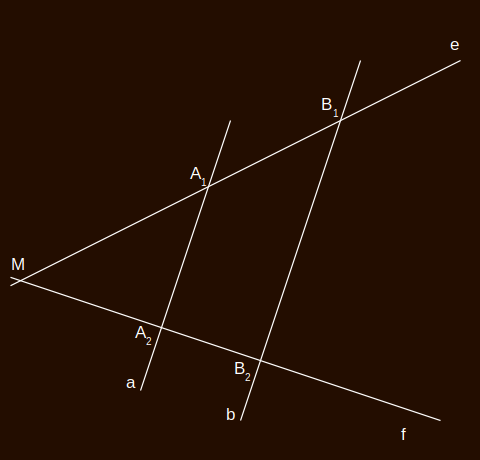\[B_2X=XM-B_2M=0\]Hiszen XM és B2M (3) és (4) alapján egyenlõk.

(6) Eszerint X ≡ B2, vagyis x ≡ b, tehát a || x ≡ b, vagyis a || b. (Kattintás.) És ezt akartuk bizonyítani.

Egy kidolgozott feladat

Feladat: Igazoljuk, hogy tetszõleges ABCD négyszög oldalfelezõ pontjai paralelogrammát alkotnak!

ábra

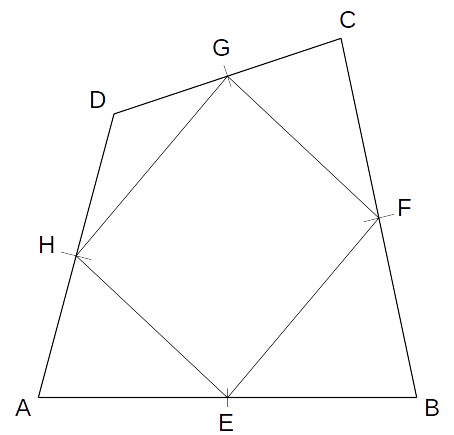
(1) Alkalmazzuk a párhuzamos szelõk tételének megfordítását az A csúcsból vézve az EH, BD szelõkre:
\[\frac{HA}{DA} = \frac12 = \frac{EA}{BA}\]Ezért (a tétel alapján) HE || DB.

(2) Alkalmazzuk a párhuzamos szelõk tételének megfordítását a C csúcsból vézve az FG, BD szelõkre:
\[\frac{GC}{DC} = \frac12 = \frac{EA}{BA}\]Ezért  GF || DB.

(3) Az (1) és a (2) alapján: HE || DB || GF.

(4) Alkalmazzuk a párhuzamos szelõk tételének megfordítását a B csúcsból vézve az EF, AC szelõkre:
\[\frac{EB}{AB} = \frac12 = \frac{FB}{CB}\]Ezért  EF || AC.

(5) Alkalmazzuk a párhuzamos szelõk tételének megfordítását a D csúcsból vézve az HG, AC szelõkre:
\[\frac{HD}{AD} = \frac12 = \frac{GD}{CD}\]Ezért  HG || AC.

(6) A (4) és az (5) alapján: HG || AC || EF.
 ábra

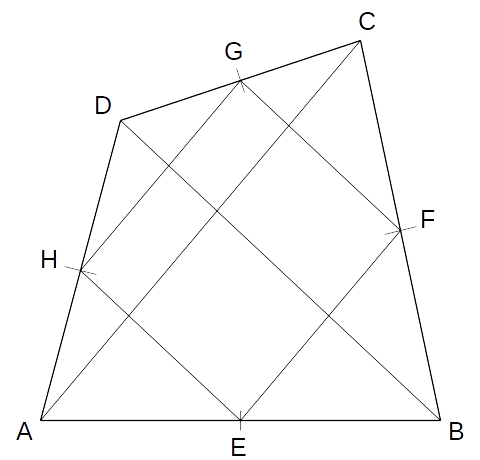(7) A (3) és a (6) pont alapján: HE || GF és HG || EF, így az EFGH négyszög szemközti oldalpárjai párhuzamosak. Tehát paralelogramma.