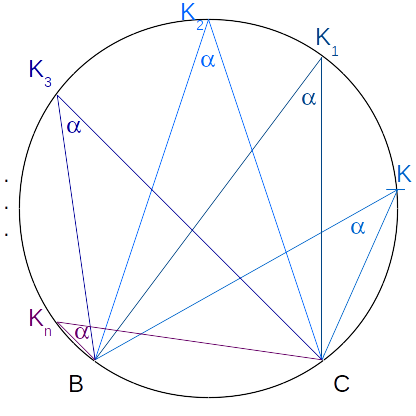
18. óra.: Középponti és kerületi szögek

Legyen adott egy O középpontú kör, és kerületén kijelölve egy BC ív.
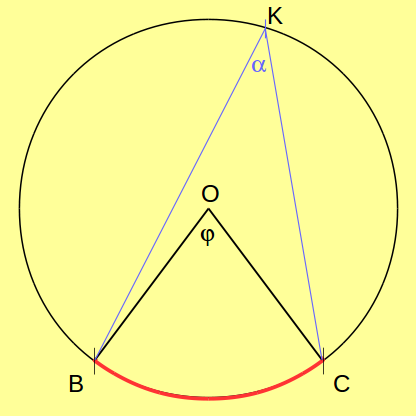
Ábra a definícióhoz
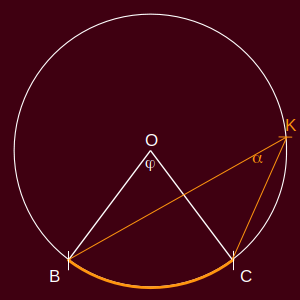
1. definíció: A BC íven nyugvó középponti szög a BOC∢, amely tartományában tartalmazza a BC ívet. (Az ábrán φ-vel jelölve.)
2. definíció: A BC íven nyugvó kerületi szög a BOK∢, amely tartományában tartalmazza a BC ívet. Itt K a kör kerületének egy tetszõleges, a BC íven kívül fekvõ pontja. (Az ábrán α-val jelölve.)

A középponti és kerületi szögek tétele: Azonos íven nyugvó kerületi szög fele a középponti szögnek:
\[\alpha=\frac\varphi{2}\](Vagy ami ugyanaz: a középponti szög a kerületi duplája: \(\varphi=2\alpha\))

Bizonyítás

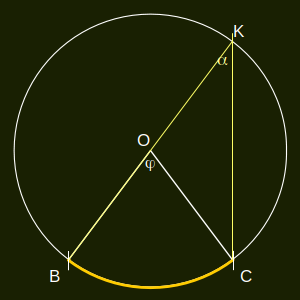
1. eset: a kör középpontja a kerületi szög szárára esik

(1) KOCΔ (katt.) egyenlõszárú (OK = OC = r), ezért OCK∢= α. (Katt.!)

(2) A KOCΔ szögösszege miatt KOC∢= 180°- 2α. (Katt.!)

(3) A φ középponti szög a KOC∢ mellékszöge, így:
\[\varphi=2\alpha,\]és ezt kellett bizonyítani.
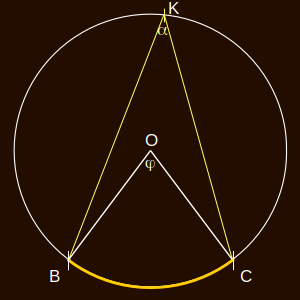
2. eset: a kör középpontja a kerületi szög tartományába esik

(1) Húzzuk meg a KO egyenest! (Katt.!) Az egyenesnek a BC ívvel alkotott metszéspontja D.

(2) α1 = BKD ∢(katt.) egy BD íven nyugvó kerületi szög, mely az (1) eset szerint szárán tartalmazza a középpontot, így a vele azonos íven nyugvó középponti szög (katt.) BOD∢= 2α1.

(3) Hasonló a helyzet a DC íven nyugvó α2 kerületi szöggel (katt.).
A hozzá tartozó középponti szög (katt.) DOC∢ = 2α2.

(4) Figyelembe véve, hogy (a K pontnál): \(\alpha_1+\alpha_2=\alpha\)
\[\varphi=2\alpha_1+2\alpha_2=2(\alpha_1+\alpha_2)=2\alpha\]Ezzel a 2. esetet igazoltuk.

3. eset: a kör középpontja a kerületi szög tartományán kívül esik

(1) Húzzuk meg a KO egyenest! (Katt.!) Az egyenesnek a BC ívvel alkotott metszéspontja P.

(2) α1 = PKB ∢(katt.) egy PB íven nyugvó kerületi szög, mely az (1) eset szerint szárán tartalmazza a középpontot, így a vele azonos íven nyugvó középponti szög (katt.) POB∢= 2α1.

(3) Hasonló a helyzet a PC íven nyugvó α2 kerületi szöggel (katt.).
A hozzá tartozó középponti szög (katt.) POC∢ = 2α2.

(4) Figyelembe véve, hogy (a K pontnál): \(\alpha_2-\alpha_1=\alpha\)
\[\varphi=2\alpha_2-2\alpha_1=2(\alpha_2-\alpha_1)=2\alpha\]Ezzel a 3. esetet is igazoltuk.

Következmény: valamely körben azonos íven nyugvó kerületi szögek egyenlõk.
Indoklás: Mindegyik ugyanannak az egyetlen \(\varphi\) középponti szögnek a fele.

Azonos íven nyugvó kerületi szõgek