46. óra: \(\frac{\sin x}x\) határértéke a 0-ban

Egy fontos határértéket vizsgálunk, mely sok lehetõséget ad majd a \(\sin\)-fv. vizsgálatára, sõt a \(\sin x\) értékének kiszámolására is. (Tetszõlegesen adott \(x\in\mathbb R\) esetén.)

Az \(f(x)=\frac{\sin x}x\) függvény képlete alapján az \(x=0\) helyen szakad, nem folytonos, így határértékét közvetlen behelyettesítésével nem tudjuk megállapítani.

Bizonyítás

Elõzetes megjegyzések:

(A) A \(\sin x\) fv. páratlansága miatt az \(f(x)=\frac{\sin x}x\) függvény páros:
\[
f(-x) = \underbrace{\tfrac{\sin(-x)}{-x} = \tfrac{-\sin x}{-x} }_{\text{Alk.: }\sin(-x)=-\sin x}= \tfrac{\sin x}{x} = f(x)
\]Ezért elég a határértéket \(x>0\) esetén igazolni - hisz negatív \(x\)-ekre ugyanaz történik a fv. párossága miatt.

(B) Mivel a határérték csak a 0 közelében lévõ értékektõl függ, elég az \(x<\frac{\pi}2\) értékekkel dolgoznunk.

Összefoglalva elõzetes gondolatainkat: Nem befolyásolja a vizsgálat eredménéyét, ha feltesszük, hogy \(0<x<\frac{\pi}2\), azaz \(x\) hegyesszög.

Lássuk a bizonyítást!

Mivel a \(\sin x\) definíciója geometriai, nem meglepõ, hogy egy geometriai ábrával operálunk. Maga a bizonyítás a rendõr-elv segítségével történik.

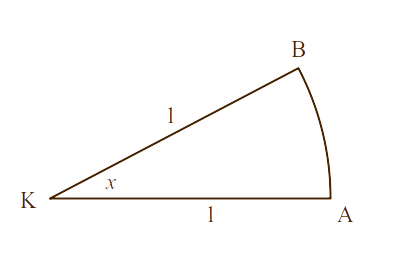
(1) Tekintsünk egy \(K\) középpontú \(x\) középponti szögû, egységsugarú körcikket! (Az ív végpontjai \(A\) és \(B\). (Ld. jobb oldali ábra!)

(2) A B pontból az AK szakaszra állított merõleges talppontját jelölje T. (Kattintás az ábrán!)

(3) A KTB derékszögû háromszög befogói a \(\sin x\) és \(\cos x\) értelmezése alapján (katt. az ábrán):
\[
\color{green}{KT=\cos x}\hphantom{000000000000000}\color{brown}{BT = \sin x}
\]

(4) Az AK szakaszra az A végpontban állított merõleges és a KB meghosszabbításának metszéspontját jelölje C. (Katt.!) (5) A \(\text{tg }x\) definíciója alapján (katt.): \(\color{blue}{AC=\text{tg }x}\)   (6) A KBT derékszögû háromszög területe (katt.): \[ \color{brown}{T_{KBT}=\frac{\sin x\cdot\cos x}{2}} \] (7) A KAB körcikk területe (katt.):  \(T_{KAB}=\frac{x}2\).   (8) A KAC derékszögû háromszög területe (katt.): \[ \color{darkblue}{T_{KAC}=\frac{\text{tg }x}{2}} \]

(9) A három terület között a tartalmazás alapján fennál a következõ reláció (katt.):
\[
\color{brown}{\frac{\sin x\cdot\cos x}{2}} < \frac{x}2 < \color{darkblue}{\frac{\text{tg }x}{2}}
\]

(10) Ezt rendezve:
\begin{equation}
\begin{split}
\frac{\sin x\cdot\cos x}{2} &< \frac{x}2 < \frac{\text{tg }x}{2} \hphantom{000000}&\big/\,\cdot 2\\\\
\sin x\cdot\cos x &< x < \text{tg }x\\\\
\text{Alkalmazzuk, hogy }\text{tg }x = \tfrac{\sin x}{\cos x}:\\
\sin x\cdot\cos x &< x < \frac{\sin x}{\cos x}&\big/\,:\sin x>0\\\\
\cos x &< \frac{x}{\sin x} < \frac{1}{\cos x}&\big/\,\frac1{(\cdot)}\text{, ami poz. számokon szig. mon. fogy}\\\\
\frac1{\cos x} &> \frac{\sin x}{x} > \cos x
\end{split}
\end{equation}
(11) A kapott egyenlõtlenség bal és jobb széle \(x\rightarrow0\) mellett ugyanoda tart - a helyettesítési értékhez, hisz a \(\cos\) fv. folytonos az \(x=0\) helyen:
\[
\lim_{x\rightarrow0}\frac{1}{\cos x} = \frac11=1 \hphantom{000000000000000}\lim_{x\rightarrow0}\cos x = 1
\]
(12) A rendõr-elv alapján így a közéjük zárt fv. is ugyanoda kell tartson, azaz:
\[
\color{darkred}{\mathbf{\lim_{x\rightarrow0}\frac{\sin x}{x}=1}}
\]

És ezt akartuk igazolni.