45. óra: Függvények folytonossága

Alapvetõ tapasztalatunk az, hogy a függvények grafikonja egy összefüggõ, 'folytonos' görbe. (1. ábra.)

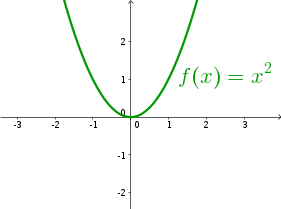1. ábra: A grafikon egy összefüggõ görbe

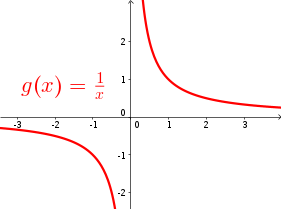2. ábra: Az értelmezési tartomány 'szakad'

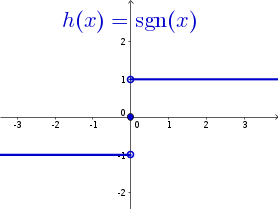3. ábra: A grafikon 'szakad', de \(D_h\) nem

Elõfordul azonban, hogy a függvény értelmezési tartományában 'rés van' - ilyenkor a grafikon biztosan nem egyetlen összefüggõ görbe (2. ábra).
Vannak olyan esetek is, amikor - bár az értelmezési tartomány összefüggõ - a grafikon mégsem az (3. ábra).

Szeretnénk ezt vizsgálni, amihez pontos definíció kéne: Mikor mondjuk azt egy függvényre, hogy folytonos?

Látható, hogy a folytonosság egy lokális tulajdonság. Egy függvény valamely pontban folytonos.

Ez szemléletesen érthetõ is, hiszen pl. a \(g(x)=\frac1x\) fv. csak az \(x_0=0\) pontban szakad, a többi helyen lehet akár folytonos is. (És ez így is van.)

Például a \(g(x)=\frac1x\) függény a pozitív számokon folytonos.

A definíció alapján egy függvény folytonossága három okból sérülhet:

1. A függvény az adott pontban nincs értelmezve (bár a pont környezetében igen). Ilyen pl. a \(g(x)=\frac1x\) az \(x=0\) helyen.
    
2. A függvény értelmezett a megfelelõ pontban, de ott nincs határértéke. Ilyen pl. a \(h(x)=\text{sgn}(x)\) az \(x=0\)-ban, mert ott az értéke 0, de határértéke nincs. (Ha 'jobbról' tartunk a 0-hoz, a határérték 1, ha balról, akkor -1; szóval határérték nincs.)
    
3. A függvénynek az adott pontban van ugyan határértéke, de az nem azonos a helyettesítési értékével.
   Ilyen függvény látszólag csak 'szándékos elrontás' útján keletkezhet.
    
   

   Egy ilyen példa az ábrán látható \(k(x)\) függvény.   Itt az \(x=1\) pontban - látszólag értelmetlenül - 'csak azért is' más értéket adunk a függvénynek, mint ami 'helyes' volna. (?)   Késõbbi tanulmányaikban látni fognak olyan eseteket, amikor ilyen függvény tényleg felléphet - szóval az ilyen esetekre is érdemes számítani...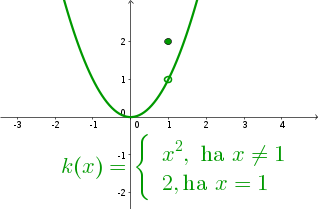

Szakadási típusok

Mindezek alapján a függvények szakadását érdemes két csoportra osztani:

1. A függvény az adott pont környezetében értelmezett (tehát felvethetõ a határérték kérdése), és ott van határértéke. Ilyenkor azt mondjuk: a függvénynek ott megszüntethetõ szakadása van.
    
   Ez egy elég szemléletes kifejezés; nincs más dolgunk, mint újradefiniálni a függvényt, és a vizsgált pontban a határértéket adni helyettesítési értéknek. (És akkor - láss csodát! - a határérték meg fog egyezni a helyettesítési értékkel - így a fv. ott folytonos lesz.)
    
2. A függvény az adott pont környezetében értelmezett (tehát felvethetõ a határérték kérdése), de ott nincs határértéke. Ilyenkor azt mondjuk: a függvénynek ott nem megszüntethetõ szakadása van.
    
   Ilyenkor nincs mit tenni, a függvény szakadása komoly.

Folytonos függvények

Mely függvényekrõl tudhatjuk biztosan, hogy folytonosak?

Soroljunk fel néhány ismert fv.-típust, melyekrõl tudhatjuk, hogy folytonosak!

1. A konstans függvények \((f(x)=c\text{, ahol }c\in\mathbb R)\) és az x függvény.
   Ez a definíció alapján közvetlenül belátható.
    
2. Folytonos függvények összege, különbsége, szorzata.
   Ennek oka az átviteli elv, amely ezekre a mûveletekre korlátlanul érvényes.
    
3. Folytonos függvények hányadosa, ha a nevezõ ott nem zérus.
   Az ok itt is az átviteli elv, csak figyelembe kell venni az osztásra érvényes korlátozást.
    
4. A polinomok a teljes értelmezési tartományukon.
   Ok: A polinomok az (i) típusú függvényekbõl a (ii) mûveletekkel vannak 'összerakva'.
    
5. Az algebrai törtfüggvények a nevezõ zérushelyén kívül.
   Ok: Az algebrai rörtek polinom hányadosai.
    
6. A sin és cos függvények teljes valós számhalmazon.
   Ezt most szemléletesen fogadjuk el! (Késõbb bizonyítjuk.)
    
7. Az exponenciális és logaritmusfüggvények a teljes értelmezési tartományukon.
   Bizonyítás késõbb.