44. óra: Függvény határértéke (ismétlés)

A hatáérték fogalmát 'visszük át' egy másik környezetre - a függvények világába.

Szemben a sorozatoknál látott \(n\rightarrow\infty\) esetben vizsgált sorozat-határértékkel, itt a függvény változója tarthat egy véges értékhez is \(\text{pl. }\left(x\rightarrow0\right)\), és hasonlóan a sorozatokhoz azt vizsgáljuk, hogy hova 'tart' eközben a függvény értéke: \(f(x)\).

Egy (igen) egyszerû példa

Tekintsük az \(f(x):=\frac{x}x\text{; }x\in\mathbb R\setminus\{0\}\) függvényt!

A függvény nyilvánvalóan értelmetlen az \(x=0\) pontban.
 
Mégis, ha az \(x\) változóval közelítünk a 0-hoz, a függvényértékek (konstans 1) az 1 számhoz tartanak.
 
Erre szeretnénk majd aztmondani, hogy az \(f(x)\) függvény határértéke a 0-ban 1:
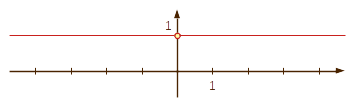Az \(f(x)\) függvény grafikonja

\[
\lim_{x\rightarrow0}f(x) = 1
\]

Általában (de nem mindig) olyan helyzeteket próbálunk 'kezelni', amikor a függvény valamely pontban úgy 'szeretne' valamely értéket 'felvenni', és bár az általunk talált definíció ezt nem engedi - ott a definiáló képlet értelmetlenné válik - mégis, mintha lenne ott valami érték, amit a függvény 'szinte felvesz' - de mégsem rendesen.
Ilyenkor szeretnénk azt mondani, hogy a függvény hatértértéke azon a helyen az a bizonyos érték.

A függvény határértékét két (ekvivalens) módon is szokás definiálni:

Mindkettõt meg kell ismernünk!

Mielõtt hozzákezdünk, meg kell érteni, hogy valamely pontban csak akkor vizsgálhatjuk a határértéket, ha a fv. értelmezési tartományában tetszõlegesen 'közel' mehetünk a vizsgált helyhez. (Az értelmezési tartománytól izoált helyen a kérdésfelvetés értelmetlen.)

Definíció: Az \(x_0\in\mathbb R\) pont torlódási pontja a \(H\subset\mathbb R\) halmaznak, ha bármely \(\varepsilon>0\) számhoz található olyan \(h\in H\) elem, amelyre \(h\ne x_0\), és \(|h-x_0|<\varepsilon\).
Megjegyzés: Valamely \(H\) halmaz egy torlódási pontja nem feltétlenül eleme \(H\)-nak.
Pl. az \(x_0=\sqrt{2}\) torlódási pontja az racionális számok halmazának - hisz bármely kicsiny környezetében vannak racionális számok, de õ maga nem racionális.

A torlódási pont szemléletes jelentése az, hogy a tekintett (H) halmaz pontjaival bármilyen közel tudunk menni úgy az \(x_0\) ponthoz, hogy azért nem 'lépünk rá' az \(x_0\)-ra.

Más szavakkal: Van olyan csupa \(H\)-beli \(h_n\ne x_0\) számokból álló sorozat, amely \(x_0\)-hoz tart.

A szekvenciális definíció

Definíció: Legyen \(f(x)\) egy valós függvény, értelmezési tartománya \(D_f\). Legyen továbbá \(x_0\) az értelmezési tartomány egy torlódási pontja.
 
Azt mondjuk, hogy az \(f(x)\) függvénynek az \(x_0\) pontban a határértéke az \(A\) szám, ha bármely \(D_f\) elemeibõl alkotott \(x_0\)-hoz konvergáló \(h_n\ne x_0\) sorozat esetén az \(f(h_n)\) sorozat \(A\) hoz tart.
Matematikai jelölésekkel:
\[
\lim_{x\rightarrow x_0}f(x) = A\text{, ha}\hphantom{0000000000}
\forall h_n\rightarrow x_0, h_n\ne x_0, h_n\in D_f\text{ esetén } f(h_n)\rightarrow A
\]

Megjegyzések: A \(h_n\) sorozat tagjainak azért kell a \(D_f\)-be esniük, hogy ott legyen értelme az \(f(h_n)\)-nek.
A \(h_n\) sorozat tagjai azért nem lehetnek egyenlõk \(x_0\)-lal, mert az \(x_0\)-ban a fv. talán nincs is értelmezve; vagy ha igen, akkor is az ott felvett értéktõl függetlenül akarjuk a határértéket definiálni.

Egy animáció, amit megmutatni, elmondani nem kell, de talán segít a megértésben... (megjelenik) ↓ (eltûnik) ↑

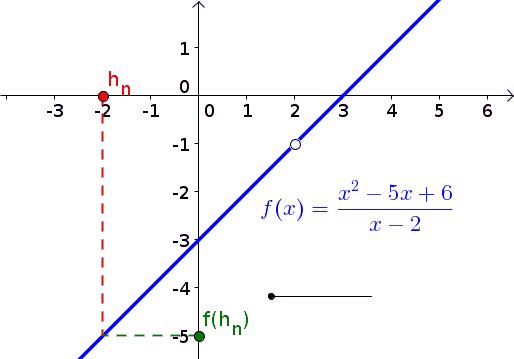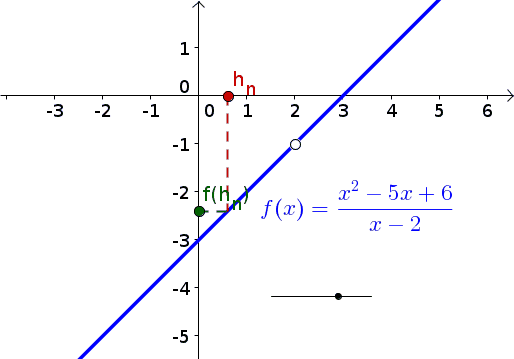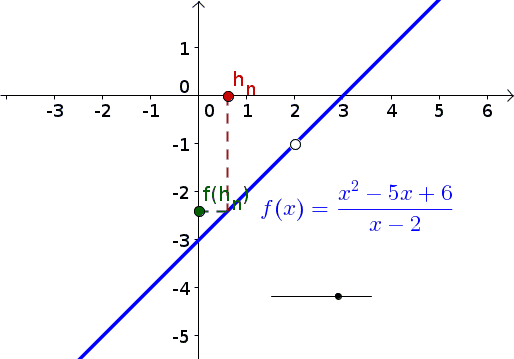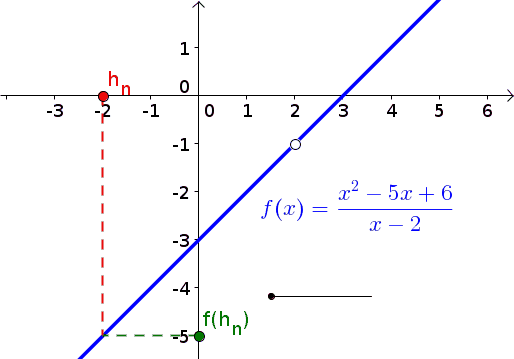
A vizsgált függvény az \(f(x)=\frac{x^2-5x+6}{x-2}\), és az animáció azt próbálja megjeleníteni, ahogy \(x\rightarrow2\) esetén a megfelelõ fv.-értékek hogyan tartanak \(-1\)-hez, a határértékhez.

 

A topológiai definíció

A most ismertett definíció ekvivalens a fentivel, de nagyon máshogy szól.

Definíció: Legyen \(f(x)\) egy valós függvény, értelmezési tartománya \(D_f\). Legyen továbbá \(x_0\) az értelmezési tartomány egy torlódási pontja.
 
Azt mondjuk, hogy az \(f(x)\) függvénynek az \(x_0\) pontban a határértéke az \(A\) szám, ha bármely \(\varepsilon>0\) számhoz található olyan \(\delta>0\) szám, amelyre:
\[
\big|\,f(x)-A\,\big|<\varepsilon\text{, ha}\hphantom{0000000000}
\big|\,x-x_0\,\big|<\delta\text{ miközben }x\in D_f\text{ és }x\ne x_0
\]

Itt tehát a közelséggel operálunk: Bármilyen elõírt \((\varepsilon>0)\) közelségben lesz a függvényérték a határértékhez, ha a változó (\(x\)) elég közel \((\delta>0)\) van az \(x_0\)-hoz. (És persze ez csak olyan \(x\)-ekre vonatkozik, ahol van fv.érték, és amelyik nem egyenlõk az \(x_0\)-lal.)

Egy újabb animáció, amirõl beszélni nem kell, de talán segít a megértésben... (megjelenik) ↓ (eltûnik) ↑

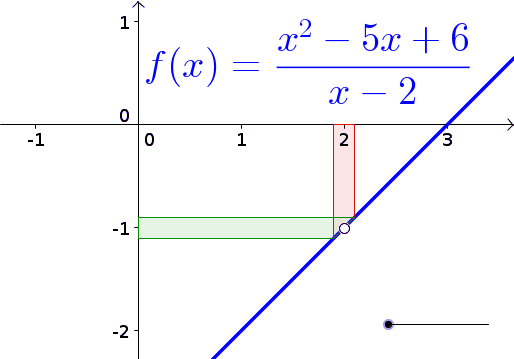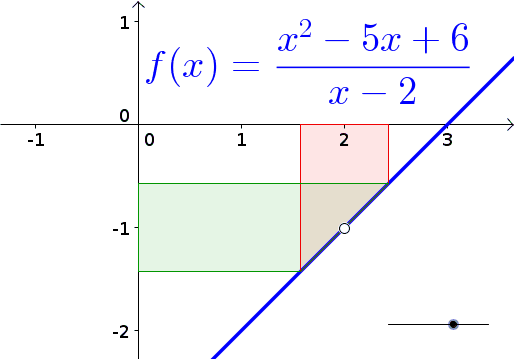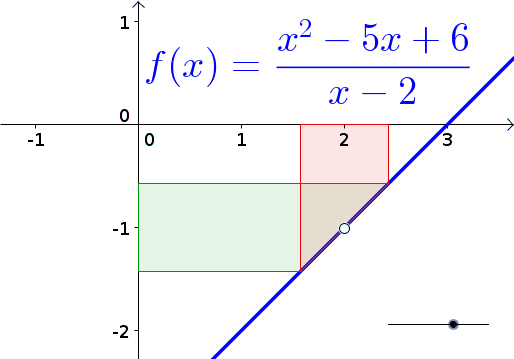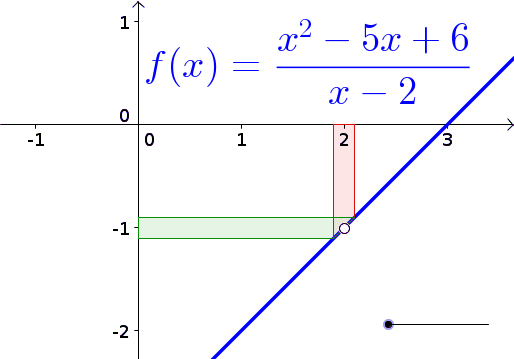
A vizsgált függvény az \(f(x)=\frac{x^2-5x+6}{x-2}\), és az animáció azt próbálja megjeleníteni, ahogy \(x\rightarrow2\) esetén a megfelelõ fv.-értékek hogyan tartanak \(-1\)-hez, a határértékhez.

BEFEJEZÉS