63. óra feladatsora: Valószínûségszûmítási gyakorlat I. (Ism.)

1. feladat: Egy kalapban négy számozott cédula van: 1, 2, 3, 4 felirattal. Véletlenszerûen kiveszünk sorban 3 db-ot, és lerakjuk egymás mellé. Pl.:

Mekkora a valószínûsége, hogy a kialakult (háromjegyû) szám osztható 6-tal?

Az 1. feladat (egy lehetséges) megoldása

Az eseménytér, \(E\)  az 1; 2; 3; 4 számok háromelemû variációinak halmaza. Elemszáma: \(|E|=4\cdot3\cdot2=24\)
(Emlék: ha egy halmazból kiválasztunk néhány elemet sorrendre tekintettel, az a kiválasztás a halmaz elemeinek egy megfelelõ elemszámú variációja.)

Jelölje \(H\) a kedvesõ eseményeket! Ezek azok a variációk, amelyeket leírva 6-tal osztható számot kapunk.

Egy szám pontosan akkor osztható 6-tal, ha

Mikor lesz a számjegyek összege 3-mal osztható? (Itt a sorrend érdektelen, hisz a számjegyek összege azt nem érzéli.)
A négy számjegyünk összege 1 + 2 + 3 + 4 = 10. Egyiket kell elhagyjunk úgy, hogy a megmaradtak 3-mal oszthatók legyenek. Elhagyhatjuk az 1-et, akkor az összeg 9, és elhagyhatjuk a 4-et, akkor az összeg 6.

A páros végzõdésre tekintettel:

A kedvezõ események halmaza: \(H=\left\{234; 324; 342; 432; 132; 312\right\}\). Elemszáma: \(|H|=6\).

A vszg.i mezõ kombinatorikus (minden elemi esemény egyformán valószínû).

Válasz: Annak valószínûsége, hogy 6-tal osztható számot húzunk:
\[
P(H) = \frac{|H|}{|E|} = \frac{6}{24} = \color{darkred}{\mathbf{\frac14}} = \color{darkred}{\mathbf{0,25}} =
\color{darkred}{\mathbf{25\%}}
\]

(Az eredmény fenti három alakjának bármelyike ugyanolyan jó.)

2. feladat: 1 m hosszú pálcát véletlenszerû helyen eltörünk. (A törés a teljes hosszon egyenletesen véletlenszerû helyen történik.)
 
Mekkora a valószínûsége, hogy a két darab és még egy fél méter hosszú pálca, mint oldalak, háromszöggé állíthatók össze?

A 2. feladat (egy lehetséges) megoldása

Jelölje \(x\) a törés helyét a \([0;1]\) intervallumban. Az eseménytér: \(E=[0;1]\). A vszg. geometriai. Az eseménytér geometriai mértéke a hosszúság: \(\text{hossz}(E)=1\).

Ha az \(x\) helyen eltörjük a pálcát, a két darab hossza: \(x\) és \(1-x\). Ha ehhez hozzáveszünk egy fél méteres darabot, a három pálca
\[
x;1-x;\tfrac12
\]A kedvezõ események halmazát jelölje \(K\).

Az \(x\in E\) akkor esik \(K\)-ba, ha az \(x;1-x;\frac12\) számok kielégítik a háromszög-egyenlõtlenséget.
(A háromszög-egyenlõtlenség szerint a három szám bármelyike kisebb kell legyen a másik kettõ összegénél.)

Praktikusan elég azt nézni, hogy a három szám közt a legnagyobb (vagy egyik legnagyobb) is kisebb a másik kettõ összegénél.

1. eset \(x<\frac12\): Ekkor \(1-x\) lesz a legnagyobb. A feltétel tehát:
\begin{equation}\begin{split}
1-x &< x + \tfrac12\\
\tfrac12 &< 2x\\
\tfrac14 &< x
\end{split}\end{equation}Ezen az ágon kapott 'jó' \(x\)-ek: \(x\in\left(\frac14;\frac12\right)\).

2. eset \(x=\frac12\): Ekkor mindhárom szakasz \(\frac12\) hosszú. Abból lehet háromszög: \(x\in K\).

3. eset \(x>\frac12\): Ekkor \(x\) lesz a legnagyobb. A feltétel tehát:
\begin{equation}\begin{split}
x &< 1-x + \tfrac12\\
2x &< \tfrac32\\
x &< \tfrac34
\end{split}\end{equation}Ezen az ágon kapott 'jó' \(x\)-ek: \(x\in\left(\frac12;\frac34\right)\).

Összefoglalva: \(K=\left(\frac14;\frac34\right). \(\text{hossz}(K)=\tfrac34-\tfrac14 = \tfrac12\).

Válasz: Annak valószínûsége, hogy a három pálcadarabból háromszöget lehessenek készíteni:
\[
P(K) = \frac{\text{hossz}(K)}{\text{hossz}(E)} = \frac{\frac12}{1} = \color{darkred}{\mathbf{\frac12}} = \color{darkred}{\mathbf{0,5}} = \color{darkred}{\mathbf{50\%}}
\]

(Az eredmény fenti három alakjának bármelyike ugyanolyan jó.)

3. feladat: Nyuszika vásárol a virágboltban 8 tulipánhagymát:
Nyuszika hazafelé menet vidáman ugrándozik, így a tulipánhagymák összekeverednek.
 
Otthon Nyuszianyuval elültetik egy virágládában, persze nem tudják melyik milyen színû. A virágok kikelnek, és kialakul egy véletlenszerû színsorrend, például:



Milyen eséllyel lesz mind a két szélsõ piros?

A 3. feladat (egy lehetséges) megoldása

Csak a piros tulipánok helyét figyeljük. (A sárgák a megmaradt helyeken vannak.)

Az eseménytér a 8 hely 3-elemû kombinációiból áll. Azt figyeljük, melyik 3 helyen áll piros tulipán.
Az eseménytér elemszáma: \(|E|=\binom83=56\). Minden elemi esemény egyformán valószínû.

Jelölje \(Sz\) azokat a kombinációkat, amikor a két szélén piros van - vagyis a kombinációban az 1. és a 8. hely is szerepel. \(Sz\) a kedvezõ események halmaza.

\(Sz\) elemeiben csak egyetlen pozíció szabad, miszerint hogy a harmadik piros hol áll. Állhat a 2., 3., ... 7 helyen. Ez hat lehetõség. \(|Sz|=6\)

Válasz: Annak valószínûsége, hogy mind a két szélre piros tulipán kerüljön:
\[
P(K) = \frac{|Sz|}{|E|} = \frac{6}{56} = \color{darkred}{\mathbf{\frac3{28}}} \approx \color{darkred}{\mathbf{0,1071}} = \color{darkred}{\mathbf{10,71\%}}
\]

4. feladat: Tamás minden reggel iskolába indul. Egy \(7^{00}\) és \(8^{00}\) közötti egyenletesen véletlen idõpontban kimegy a buszmegállóba. Vár a buszra. Türelmetlen ember, ha 6 percig nem jön semmi, hazamegy, visszafekszik, aznap nem megy iskolába.

Tamásnak két busz jó:
A menetidõ az iskoláig 16 perc. (A buszra szállás pillanatától az iskolába beérésig.)

A) Mekkora a valószínûsége annak, hogy egy nap Tamás iskolába megy?

B) Mekkora az esélye, hogy Tamás bemegy, de késik? (8-ra kellene beérnie.)

A 4. feladat (egy lehetséges) megoldása

Az idõt mérjük a 7 óra után eltelt percekben! Eszerint az eseménytér, Tamás érkezése a megállóba, \(E=[0;60]\).
Az \(E\) geometrikus vszg. van. Geometriai mérték a hosszúság: \(\text{hossz}(E)=60\).

Jelölje \(A\) azt az eseményt, hogy Tamás iskolába megy. Az \(A\) esemény a maximálisan 6 perces váakozási idõt figyelembe véve a buszok indulásától visszaszámolva 6 percen belüli intervallumokból áll.
\begin{equation}\begin{split}
A&=[0;3]\cup[9;15]\cup[17;23]\cup[24;30]\cup[24;30]\cup[37;45]\cup[54;60]\\
\text{hossz}(A)&=3+6+6+6+8+6 = 35
\end{split}\end{equation}

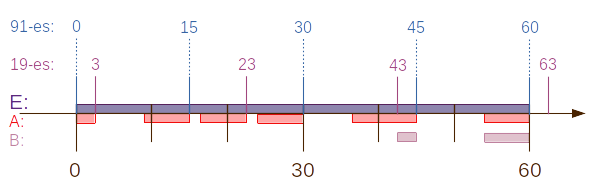
Jelölje \(B\) azt az eseményt, hogy Tamás iskolába megy, de késik. A \(B\) esemény része \(A\)-nak.
Tamás akkor késik el, ha a 45-kor vagy a 60-kor érkezõ buszt éri el. Ennek megfelelõen:
\begin{equation}\begin{split}
B&=(43;45]\cup[54;60]\\
\text{hossz}(B)&=2+6 = 8
\end{split}\end{equation}

Válasz az A kérdésre: Annak valószínûsége, hogy Tamás iskolába megy:
\[
P(A) = \frac{\text{hossz}(A)}{\text{hossz}(E)} = \frac{35}{60} = \color{darkred}{\mathbf{\frac7{12}}}  \approx\color{darkred}{\mathbf{0,5833}} = \color{darkred}{\mathbf{58,33\%}}
\]

Válasz a B kérdésre: Annak valószínûsége, hogy Tamás késve ér az iskolába:
\[
P(B) = \frac{\text{hossz}(B)}{\text{hossz}(E)} = \frac{8}{60} = \color{darkred}{\mathbf{\frac2{15}}}  \approx\color{darkred}{\mathbf{0,1333}} = \color{darkred}{\mathbf{13,33\%}}
\]

(Az eredmények fenti három-három alakjának bármelyike ugyanolyan jó - bár a közönséges tört a pontos.)

5. feladat: Útépítõ munkások fasort ültetnek az út mellé. Fenyõk és bükkfák kerülnek oda, összesen 7 db, sorban egymás mellé, véletlenszerûen (ahogy jön). (Végtelen a készlet mindkettõbõl, és mindig ugyanannyi az esélye, hogy ez vagy az jön.) Például:

Mekkora annak a valószínûsége, hogy bükkfák nem kerülnek egymás mellé?

A 5. feladat (egy lehetséges) megoldása

A nyolc hely mindegyikén fenyõ, vagy bükk áll. Ez két-két lehetõség mindenütt.

Az eseménytér: \(E=\left\{\text{2 elem 7-edrendû ismétléses variációi}\right\}\).
(Emlék: Ha \(n\) különbözõ elembõl kiválaszunk \(k\) db-ot sorrendre tekintettel, az ismétlést is megengedve, kapjuk az \(n\) elem egy \(k\)-adrendû ismétléses variációját.\(n\) elem \(k\)-adrendû ismétléses variációinak száma: \(V_n^k=k^n\).)

Az eseménytér elemszáma: \(|E|=2^7=128\). Az eseménytéren kombinatorikus a valószínûség.

A kedvezõ események halmazát jelölje \(K\), azokból az ismétléses variációkból áll, amelyekben nincs egymás mellett bükkfa. Ennek elemszámát kell megállapítanunk. Ezt tanulási céllal többféleképpen is megnézzük.

1. módszer: Az összes elem felsorolása. Jelölje B a bükkfát, F a fenyõt! Az eseteket a bükkfák száma szerint csoportosítva írjuk fel:

\(|K|=1+7+15+10+1=34\).

2. módszer: Bolyongással. Készítsünk egy bolyongási táblát, amelyben jobbra és lefele léphetünk sakktáblaszerûen.  A jobbra lépés jelentse azt, hogy fenyõ jön, a lefele lépés jelentse azt, hogy bükk jön.

A tábla bal felsõ sarkában 1 áll. Ez azt jelenti, hogy 0 db fát 1 -féleképp helyezhetünk el a feltételeknek megfelelõen. Innen indulunk, és töltjük ki a bolyongási tábla celláit. A cellák értéke a többi cellából számolható rekurzívan.

Szabályok:

  1. szabály: Bármely cellába szabadon léphetünk a tõle balra álló cellból, mert az jobbralépés, tehát fenyõ, ami a feltételt nem sértheti. Tehát egy cellába beírható a tõle balra álló értéke összeadandóként. (Ha tõle balra nincs semmi, akkor az összeadandó is semmi.)
  2. szabály: A fölöttünk álló cellából csak akkor jöhetünk ide, ha oda nem fölülrõl jöttünk. (Mert ha oda felülrõl érkeztünk, akkor éppen most tettünk le egy bükkfát, tehát ha lefele továbbmennénk az még egy bükkfát jelentene. Az pedig tilos.) Azt a részét adhatjuk tehát hozzá a felettünk álló cellának a mienkhez, amely a felettünk álló cella balról jövõ része.
    Vagyis a balra felettünk átlósan álló cella értéke írható ide összeadandóként.

A séta akkor ér véget, ha hetet lépünk (ezeket a helyeket az ábrán kiemeltem). A tábla praktikusan vízszintesen max. 7, függõlegesen max. 4 lépésnyire kell kiterjedjen, mert több fenyõ, ill. bükk nem játszik.

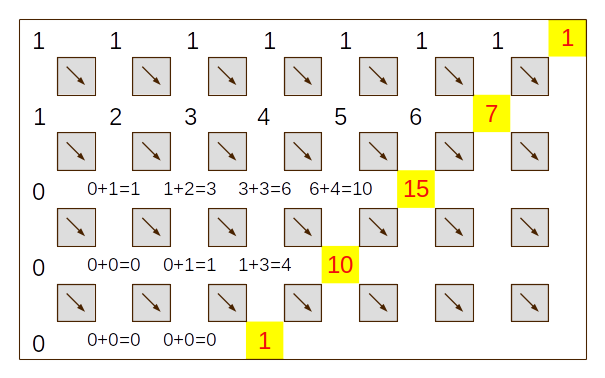
A lehetõségek száma a szabályos hétlépéses utak végpontjaiba írt számok összege:
\[
|K| = 1+7+15+10+1=34
\]

3. módszer: Egy Fibonacci-szerû sorozat alkalmazásával.

Legyen \(k_n\) annak száma, ahányféleképp \(n\) db fa (fenyõ v. bükk) elhelyezhetõ úgy, hogy bükk nem kerül egymás mellé!

\(k_0=1\), \(k_1=2\), a rekurzió: \(k_{n+1} = k_n+k_{n-1}\). (Ezt piros/kék gyöngyökkel tanultuk, nem részletezném...)

\begin{equation}\begin{split}
k_0 &= 1\\
k_1 &= 2\\
k_2 &= 3\\
k_3 &= 5\\
k_4 &= 8\\
k_5 &= 13\\
k_6 &= 21\\
k_7 &= 34
\end{split}\end{equation}\(|K| = 34\)

Válasz: Annak valószínûsége, hogy a fasorban ne kerüljön egymás mellé bükk:
\[
P(K) = \frac{|K|}{|E|} = \frac{34}{128} = \color{darkred}{\mathbf{\frac{17}{64}}} \approx \color{darkred}{\mathbf{0,2656}} = \color{darkred}{\mathbf{26,56\%}}
\]

6. feladat:

 Lajos, a szórakozott kis matematikus és Julcsi, egy zeg-zugos utcácskákból álló kisvárosban laknak és ugyanabba az iskolába járnak. Reggeli útjuk az iskolába menet (a zeg-zug-on) egy kis térnél fut össze, ahol minden reggel egy egyenletesen véletlenszerû 7:00 - 8:00 közti  idõpontban haladnak át. Kinek-kinek, ahogy sikerül.

(Minden idõpont egyenlõen valószínû mindkettõjük számára, egymástól függetlenül, de 7 és 8 közé esik, az biztos.)

Lajos az érkezésekor megnézi az óráját, és annyit vár Julcsira, amennyi a 8-ig hátrlévõ idõ fele. Pl. ha még fél óra van hátra 8-ig, akkor negyed órát vár...
Ha addig Julcsi nem jön, elmegy az iskolába.

Julcsi 5 percet vár Lajosra, de legkésõbb 8-ig. Ha addig Lajos nem jön, megy az iskolába.

Mekkora az esélye, hogy Julcsi és Lajos találkoznak?

A 6. feladat (egy lehetséges) megoldása


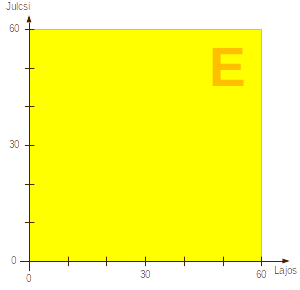
Az eseményteret jelölje E. Az idõt a 7 óra után eltelt percekben mérjük.

A történetet két, egymástól teljesen függetlenül alakuló 0-60 közti véletelen szám alakítja ki.

Ez jól ábrázolható a koordinátarendszer \([0;60]\times[0;60]\) koordinátájú pontjaival. Lajos érkezése az x-, Julcsié az y-koordináta.

Az eseménytér geometriai mértéke a terület:
\[
T_E = 60\cdot60 = 3600
\]
A kedvezõ események részhalmazát (ha tehát Lajos és Julcsi találkoznak) jelölje K.

Az eseménytér fõátlójában (ahol y = x) helyezkednek el azok az elemi események, amelyeknél Lajos és Julcsi egyszerre érkeznek. (Ezek jók.)

K-t két részre bontjuk.

K1 legyen az a rész, amikor Lajos érkezik elõbb. Lajos vár. Ha addig Julcsi megjön, akkor jó. Meddig vár Lajos?
Ha 0-kor érkezik, 30-ig vár...
... ha 10-kor érkezik, 35-ig vár...
... ha 20-kor érkezik, 40-ig vár...
...
... ha 50-kor érkezik, 55-ig vát...
... ha 60-kor érkezik, 60-ig vár. (Vagyis nem vár.)

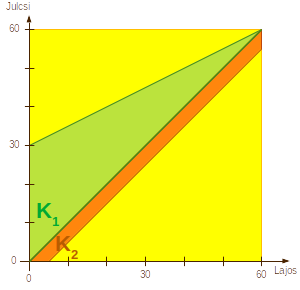Általában, ha Lajos az \(x\) idõpontban érkezik, akkor a várakozás végpontját így számolja ki:
\[
x+\tfrac{60-x}2 = x + 30 - \tfrac{x}2 = \tfrac{x}2 + 30
\]A várakozási végpontok (amin belül Julcsi jó lenne, ha megérkezne) egy egyenessé állnak össze, mely az
\[
f(x) = \tfrac{x}2 + 30
\]függvény grafikonja. Tehát \(K_1\) a szögfelezõ és az \(f(x)\) grafikonja közé esõ része \(E\)-nek.

\[
T_{K_1} = \tfrac{30\cdot60}2 = 900
\]K2 legyen az a rész, amikor Julcsi érkezik elõbb, de Lajos is megjön 5 percen belül (v. legkésõbb 5' múlva).
\[
T_{K_2} = \tfrac{60\cdot60}2 - \tfrac{55\cdot55}2 = \tfrac{3600-3025}2 = \tfrac{575}2
\]A K halmaz területe a két terület összege:
\[
T_K = T_{K_1} + T_{K_2} = 900 + \tfrac{575}2 = \tfrac{1800}2 + \tfrac{575}2 = \tfrac{2375}2
\]A keresett valószínûség:
\[
P(K) = \tfrac{T_K}{T_E} = \tfrac{\frac{2375}2}{3600} = \tfrac{2375}{7200} = \tfrac{95}{288} \approx 0,3299
\]Válasz: Annak valószínûsége, hogy Julcsi és Lajos találkoznak 0,3299 vagy 32,99%.