Szerkesztések

Az elindított GeoGebra programban legyen nyitva az Algebra ablak és a Rajzlap. A tengelyekre és a rácsra egyenlőre nincs szükség. Tedd láthatóvá a Formázó léc-et.

Általános háromszög szerkesztése

Szerkessz háromszöget, állítsd át az objektumok láthatóságát, feliratát, nevezd át az oldalakat, csúcsokat, a poligont.
Jelenítsd meg a Parancssort, definiáld a háromszög területét, és írasd is ki. Vedd fel a háromszög szögeit, és mozgasd a csúcsokat! $$\ \ $$

Háromszögek

$$\ \ $$

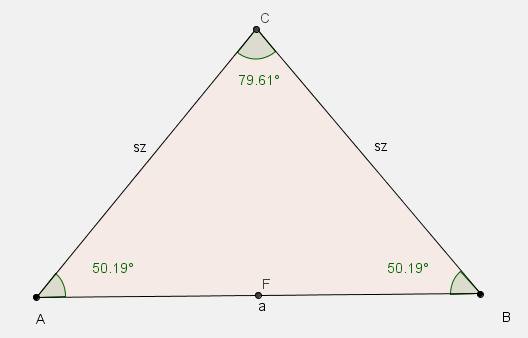
Szabályos háromszög szerkesztése

• Szerkessz szabályos háromszöget, csak a szabad pontok mozgathatók.


• Szerkeszd meg a háromszög középpontját, és tükrözd arra a háromszöget. Színezd kedved szerint.

$$\ \ $$

Derékszögű háromszög szerkesztése

$$\ \ $$

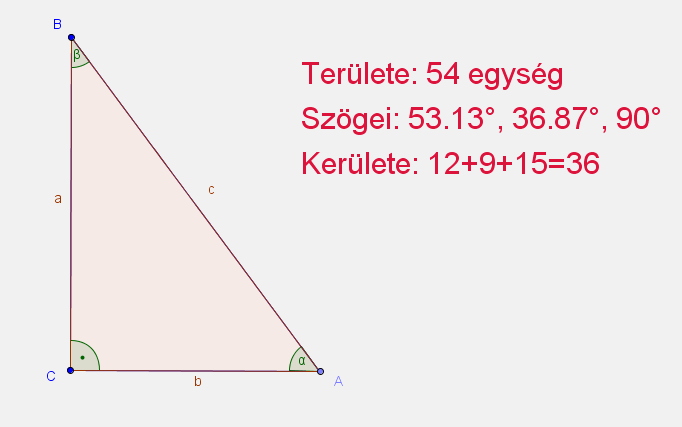
• Szerkessz derékszögű háromszöget, melynek befogói 12 és 9 egység hosszúak.


• Definiáld a sokszöget, a szögeit, a területét.


• Írasd ki a háromszög területét, kerületét és szögeit!
  

$$\ \ $$
$$\ \ $$

Egyenlő szárú háromszög szerkesztése

$$\ \ $$

• Szerkessz egyenlő szárú háromszöget, melynek alapja 10 egység, magassága pedig 6 egység.

$$\ \ $$

Négyszögek

Paralelogramma

$$\ \ $$

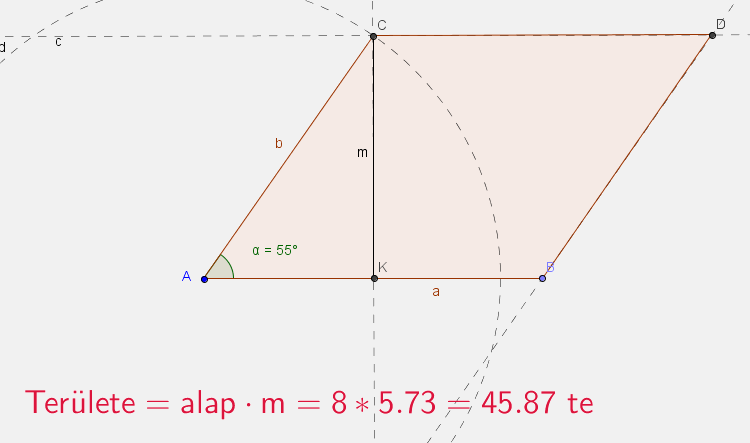
• Szerkessz paralelogrammát, ha adott két oldala: 8 és 7 egység, és a közbezárt szög $55^\circ $


• Definiáld a sokszöget, a szögeit, a területét.


• Írasd ki a paralelogramma területét!
  

$$\ \ $$
$$\ \ $$ $$\ \ $$

Trapéz

$$\ \ $$

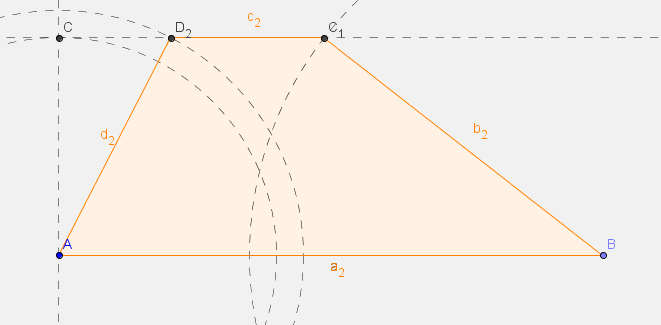
• Szerkessz trapézt, ha alapja 10, magassága 4 egység, a szárak hossza pedig 4.5 és 6.5 egység!


• Hány megoldás van?

$$\ \ $$
$$\ \ $$

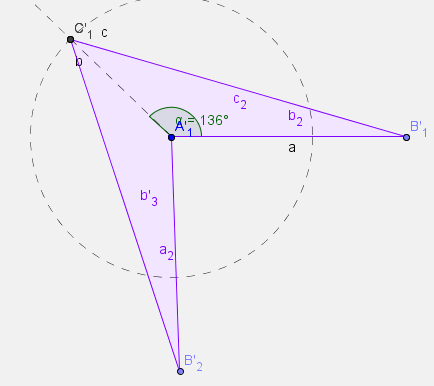
Deltoid

$$\ \ $$

• Szerkessz tompaszögű háromszöget, melynek 2 oldala 10 és 6 cm, közbezárt szöge 135 fok.


• Tükrözd a leghosszabb, majd a legrövidebb oldalára mindkét poligont emeld ki más-más színnel.


• Milyen sokszögeket kaptál?

$$\ \ $$
$$\ \ $$

Sokszögek

Forgó

$$\ \ $$

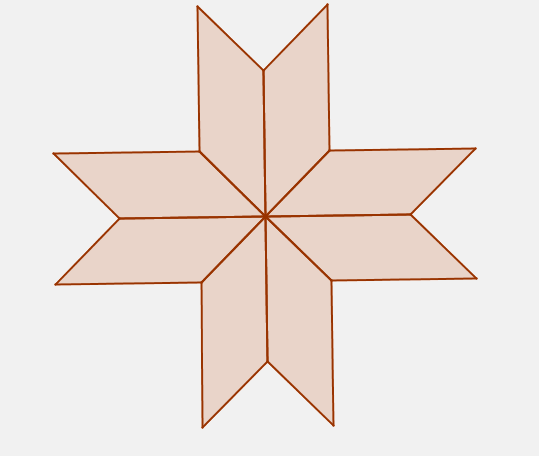
• Készítsd el az alábbi ábrát a GeoGebra program eddig tanult funkciói segítségével!

$$\ \ $$

Csillagötszög

$$\ \ $$

• Készítsd el az alábbi ábrát! $$\ \ $$

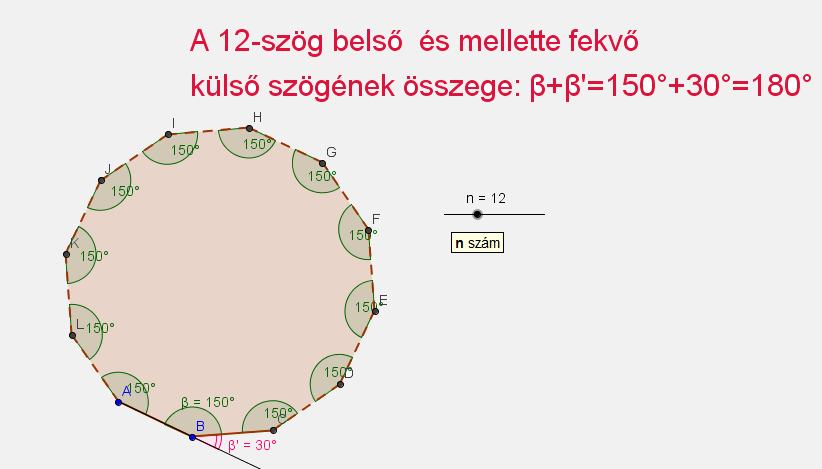
Szabályos sokszög

$$\ \ $$

• Vegyél fel egy szabályos 12 szöget. Vedd fel a szögeit: Szög[Alakzat] parancs.


• Végezd el a feladatot általánosan is: Vegyél fel egy csúszkát. 100 széles, egész 3-30-ig. Alapérték=12


• Definiáld át a sokszöget: Sokszög[A,B,n] Változtasd a csúszkán az értéket. Animáld!


• Vegyél fel egy A-ból induló félegyenest! Vedd fel a sokszög egy külső szögét! Csak az értéke látszódjon. Írasd ki a képernyőre a két szög összegét formulákkal!
  

$$\ \ $$

Geometriai transzformációk, ponthalmazok

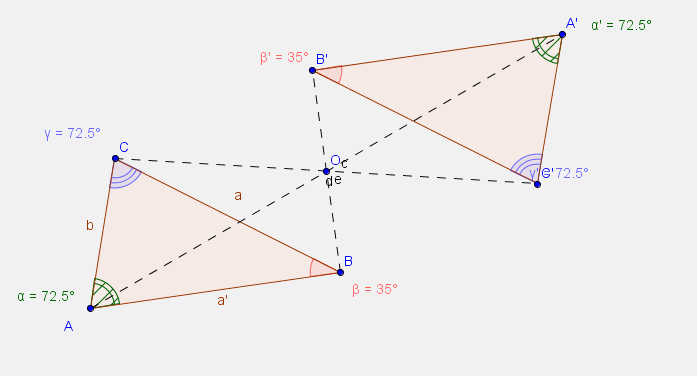
Középpontos tükrözés

$$\ \ $$

• Vegyél fel egy 35 fokos szögű tetszés szerinti háromszöget és rajta kívül egy O pontot. Tükrözd a háromszöget az O pontra.


• Mozgasd az O pontot, és a csúcsokat is. Fogalmazd meg a középpontos tükrözés tulajdonságait!


• Jelöld meg azonos színnel és díszítéssel az egyenlő nagyságú szögeket! Milyen szögpárok ezek?
  

$$\ \ $$

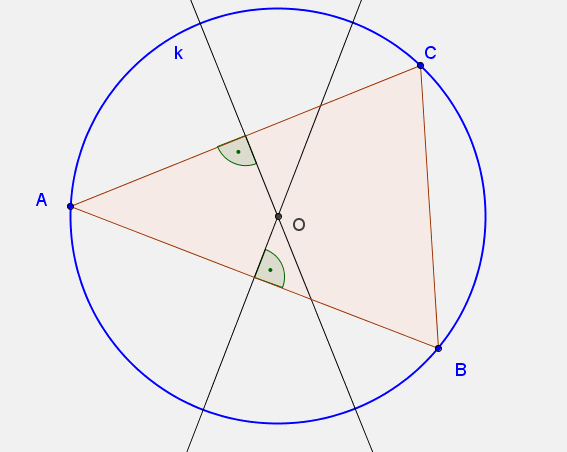
Háromszög köréírt és beírt köre

$$\ \ $$

• Vegyél fel egy általános háromszöget, és szerkeszd meg a köréírt körét! Mozgasd a csúcsokat! Mit mondhatunk a köréírt kör középpontjáról?


• Próbáld ki a program köré írt kör funkcióját is!


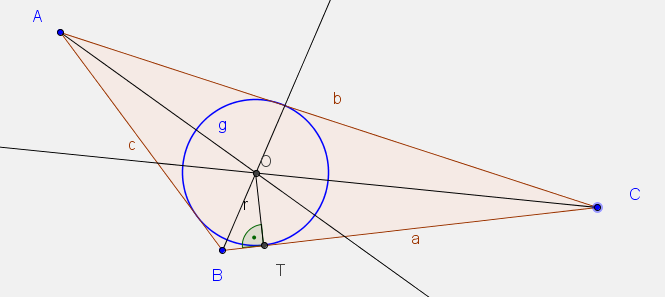
• Egy másik ábrában szerkeszd meg a háromszög beírható körét!

$$\ \ $$

Háromszög területe

$$\ \ $$

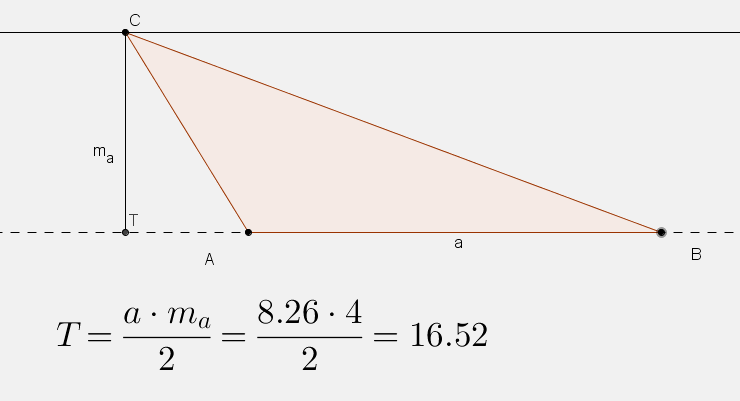
• Vegyél fel egy AB szakaszt, és azon fektess egy szaggatott egyenest!


• Az A pontba állíts merőlegest és 4 egység sugarú körrel metszd el. Az egyik metszéspontba húzz a szaggatott egyenessel párhuzamost! Ezen vedd fel a C mozgó pontot, és vedd fel az ABC háromszöget!


• C-ből állíts merőlegest az AB- oldal egyenesére, és ott vedd fel a háromszög ma-val jelölt AB oldalhoz tartozó magasságát!
• Definiáld a háromszög területét! Írasd ki formulákkal!


• Animáld a C pontot! Mit állapíthatunk meg?

$$\ \ $$

Forgatás

$$\ \ $$

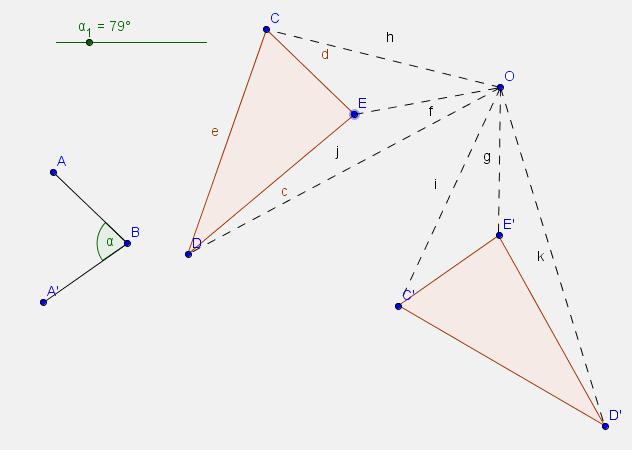
• Vegyél fel egy csúszkát, melyen az $\alpha$ szög 0 és 360 fok között változik.


• Vegyél fel egy A és egy B pontot, (B a forgatás középpontja) és definiálj egy $\alpha$ szögű elforgatást. Szerkeszd meg az AB és az A'B szakaszokat


• Vegyél fel egy CDE háromszöget és rajta kívül egy O pontot. Forgasd el a háromszöget az O pont körül $\alpha$ szöggel. Kösd össze a kp-tal az eredeti és a képpontokat


• Milyen tulajdonságai vannak a forgatásnak?

$$\ \ $$

Középpontos hasonlóság

$$\ \ $$

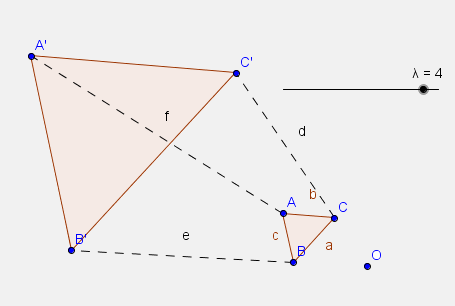
• Vegyél fel egy csúszkát, melyen az érték -5 és 5 között 0.5-es egységenként változzon, és vegyél fel egy O pontot!
  


• Szerkeszd meg az ABC háromszöget!


• Szerkeszd meg az ABC háromszög középpontosan hasonló képét ahol a $ \lambda$ értékét (a hasonlóság arányát )a csúszkán állítod!


• Kösd össze az eredeti és a képpontokat szaggatott vonallal!
  Milyen tulajdonságai vannak a középpontos hasonlóságnak?

$$\ \ $$