
126. óra: Függvénytani gyakorlatok
1. feladat: Ábrázolja és
írja le az alábbi függvényt:
\[
f(x) = \frac{-3}{x-4}+5,\hphantom{000}x\in\mathbb R\setminus\{4\}
\](A leírásban kérem az értelmezési tartományt, értékkészletet, növekedési viszonyokat, szélsõértéket - hely, érték, zérushelyet.)
\[
f(x) = \frac{-3}{x-4}+5,\hphantom{000}x\in\mathbb R\setminus\{4\}
\](A leírásban kérem az értelmezési tartományt, értékkészletet, növekedési viszonyokat, szélsõértéket - hely, érték, zérushelyet.)
Megoldás: (megjelenik)
↓ (eltûnik)
↑
Késõbb...
2. feladat: Ábrázolja és
írja le az alábbi függvényt:
\[
f(x) = -\frac12x^2-4x-6,\hphantom{000}x\in\mathbb R
\](A leírásban kérem az értelmezési tartományt, értékkészletet, növekedési viszonyokat, szélsõértéket - hely, érték, zérushelyet.)
\[
f(x) = -\frac12x^2-4x-6,\hphantom{000}x\in\mathbb R
\](A leírásban kérem az értelmezési tartományt, értékkészletet, növekedési viszonyokat, szélsõértéket - hely, érték, zérushelyet.)
Megoldás: (megjelenik)
↓ (eltûnik)
↑
Késõbb...
3. feladat: Ábrázolja és
írja le az alábbi függvényt:
\[
f(x) = \frac{x+3}{x-2},\hphantom{000}x\in\mathbb R\setminus\{2\}
\](A leírásban kérem az értelmezési tartományt, értékkészletet, növekedési viszonyokat, szélsõértéket - hely, érték, zérushelyet.)
\[
f(x) = \frac{x+3}{x-2},\hphantom{000}x\in\mathbb R\setminus\{2\}
\](A leírásban kérem az értelmezési tartományt, értékkészletet, növekedési viszonyokat, szélsõértéket - hely, érték, zérushelyet.)
Megoldás: (megjelenik)
↓ (eltûnik)
↑
Késõbb...
4. feladat: Grafikonja
alapján adja meg az alábbi függvények képletét és értékkészletét!
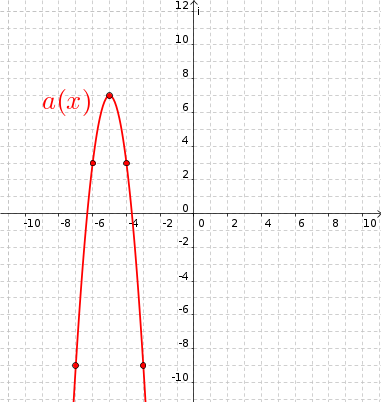



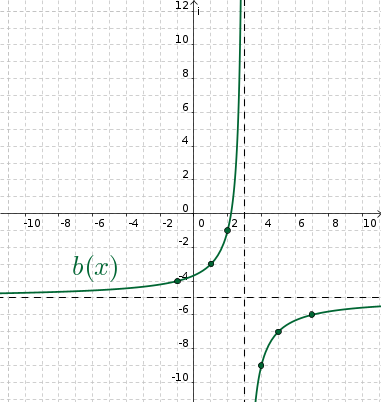
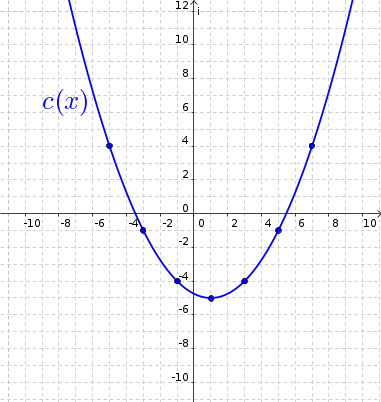



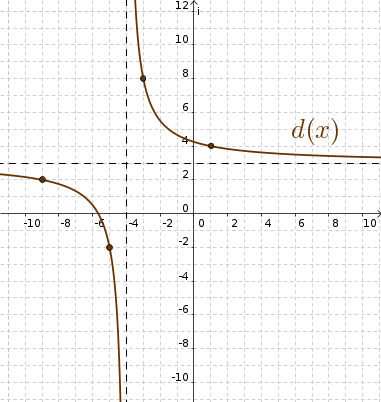










Megoldás: (megjelenik)
↓ (eltûnik)
↑
Késõbb...



