
107. óra gyakorlat: Az abszolútérték-függvény és transzformációi
1. feladat: Ábrázolja az
alábbi függvényt!
\[
a(x) = -\tfrac34\big|\,x-2\,\big|+4,\hphantom{000}x\in\mathbb R
\]Adja meg a függvény
\[
a(x) = -\tfrac34\big|\,x-2\,\big|+4,\hphantom{000}x\in\mathbb R
\]Adja meg a függvény
- értékkészletét,
- növekedési viszonyait,
- szélsõértékét (ha van)
- szélsõérték típusa (max. vayg min.)
- értéke,
- helye,
- zérushelyét (ha több van, mindet, ha egy sincs, akkor mondja ki, hogy nincs neki)!
Megoldás: (megjelenik)
↓ (eltûnik)
↑
Késõbb...
2. feladat: A \(g(x)\)
és \(h(x)\) az \(\big|\,x\,\big|\) függvény transzformáltjai.
Grafikonjuk alapján adja meg a \(g(x)\) és a \(h(x)\) függvény képletét!
s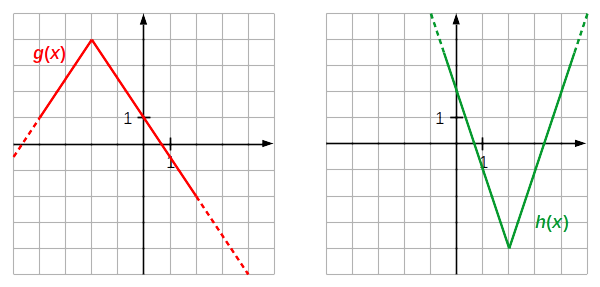

Megoldás: (megjelenik)
↓ (eltûnik)
↑
Késõbb...
| Vannak olyan esetek, amikor egy ilyen fv. nem
ateljes valós számhalmazon értelmezett. Például az alábbi
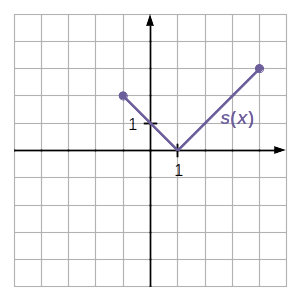
\(s(x)\) fv. (ld. ábra): \[ s(x) = \big|\,x-1\,\big|,\hphantom{000}x\in\left[-2;4\vphantom{\tfrac00}\right] \]A fv. értékkészlete \(R_s=\left[0;3\vphantom{\tfrac00}\right]\). Az értékkészletnek van legnagyobb eleme (ez a 3), ezt joggal nevezhetjük a fv. maximális értékének, vagyis maximumértéknek. (Ez a legnagyobb érték, amit a fv. egyáltalán felvehet.) Az a hely, ahol ezt megteszi (az x = 4) a fv. maimumhelye. Akkor is, ha a 'szélén' veszi fel. A fv. szélsõértékei tehát: Maximum értéke: 3, helye: 4, Minimum értéke: 0, helye 1. |
 |
3. feladat: Ábrásozja és
jellemezze szélsõérték szempontjából az alábbi függvényegeket! (Max.
érték, hely, minimum érték, hely; és ha valamelyik típusú szélõértéke
nincs, akkor azt is jelentse ki!. (Pl.: a függvénynek nincs
maxiuma.)
\(A(x)=\big|\,x-3\,\big|-1,\hphantom{000}x\in\left[-2;5\vphantom{\tfrac00}\right]\)
\(B(x)=-\big|\,x+2\,\big|+3,\hphantom{000}x\in\left[-5;1\vphantom{\tfrac00}\right]\)
\(C(x)=2\big|\,x-1\,\big|-4,\hphantom{000}x\in\left(-1;3\vphantom{\tfrac00}\right]\)
\(A(x)=\big|\,x-3\,\big|-1,\hphantom{000}x\in\left[-2;5\vphantom{\tfrac00}\right]\)
\(B(x)=-\big|\,x+2\,\big|+3,\hphantom{000}x\in\left[-5;1\vphantom{\tfrac00}\right]\)
\(C(x)=2\big|\,x-1\,\big|-4,\hphantom{000}x\in\left(-1;3\vphantom{\tfrac00}\right]\)
Megoldás: (megjelenik)
↓ (eltûnik)
↑
Késõbb...
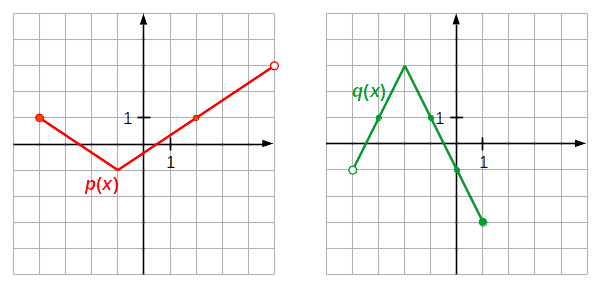
4. feladat: A \(p(x)\) és
\(q(x)\) az \(\big|\,x\,\big|\) függvény transzformáltjai. Grafikonjuk
alapján adja meg a \(p(x)\) és a \(q(x)\) függvény képletét, értelmezési
tartományát és értékkészletét!

Megoldás: (megjelenik)
↓ (eltûnik)
↑
Késõbb...



