1. feladat: Vegyen fel két egymásra merõleges egyenest: \(e\) és \(f\), valamit a metszéspontjuktól 2 cm-re az \(e\)-n egy \(E\) pontot!
Tekintsük a következõ halmazokat:
\[
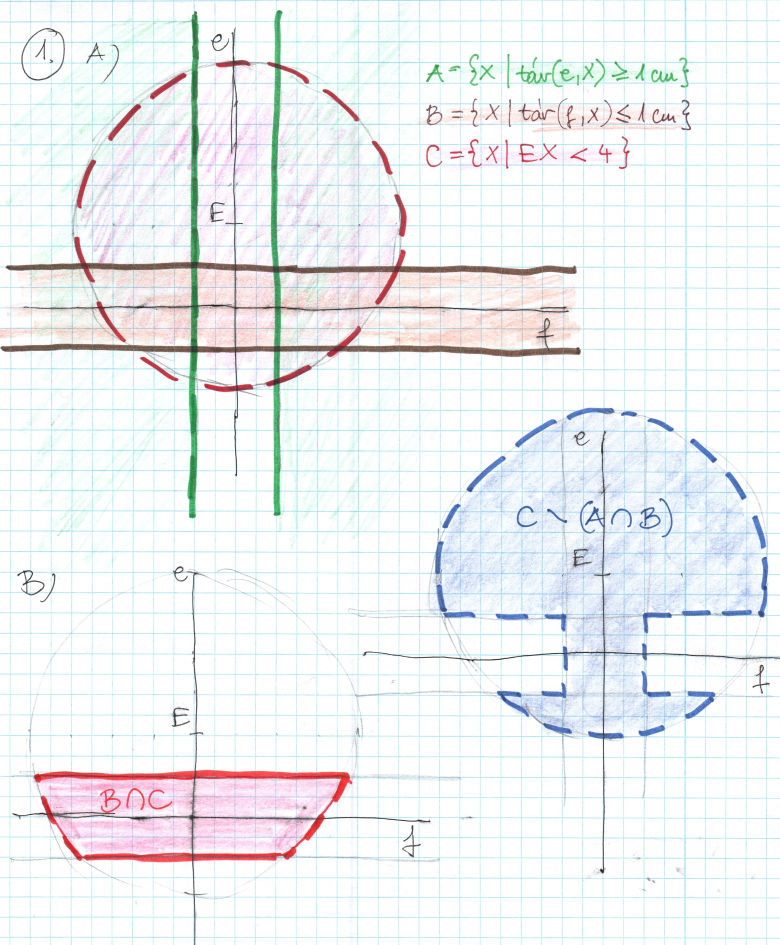
A=\left\{X\in\text{sík}\,\big|\,\text{táv}(e,X)\ge1\,\text{cm}\right\}\hphantom{00000}
B=\left\{X\in\text{sík}\,\big|\,\text{táv}(f,X)\le1\,\text{cm}\right\}\hphantom{00000}
C=\left\{X\in\text{sík}\,\big|\,EX<4\,\text{cm}\right\}
\]
A) Ábrázolja az \(A\), \(B\) és \(C\) halmazokat.
 
B) Ábrázolja a \(B\cap C\) halmazt.
 
C) Ábrázolja a \(C\setminus(A\cap B)\) halmazt.

2. feladat: Legyen \(H=\left\{0;1;2;3;4;5;6;7;8;9\right\}\) (egy tízelemû halmaz).
 
A) Hány részhalmaza van \(H\)-nak összesen?
 
B) Hány háromelemû részhalmaza van \(H\)-nak?
 
C) Hány olyan háromelemû részhalmaza van \(H\)-nak, amelyben van páratlan szám? (Válaszát röviden indokolja!)
 
D) Hány olyan háromelemû részhalmaza van \(H\)-nak, amelyben legalább két páratlan szám van? (Válaszát röviden indokolja!)

3. feladat: Vegyen fel a síkon két egymástól 4 cm távolságra fekvõ pontot, nevük: \(P\) és \(Q\).
Tekintsük a következõ halmazokat:
\[
K=\left\{X\in\text{sík}\,\big|\,QX<PX\right\}\hphantom{00000}
L=\left\{X\in\text{sík}\,\big|\,PX<2\,\text{cm}\right\}\hphantom{00000}
M=\left\{X\in\text{sík}\,\big|\,QX\le2\,\text{cm}\right\}
\]
A) Ábrázolja a \(K\), \(L\), \(M\) halmazokat.
 
B) Ábrázolja az \(M\setminus L\) halmazt.
 
C) Ábrázolja a \(K\cap(M\setminus L)\) halmazt.

4. feladat: 32-lapos magyar kártyából kivesszük a VII-es, VIII-asokat. Marad 24 lap
A 24 lapból 4-et osztanak nekünk.
 
A következõ kérdésekre adott válaszait röviden indokolja!
 
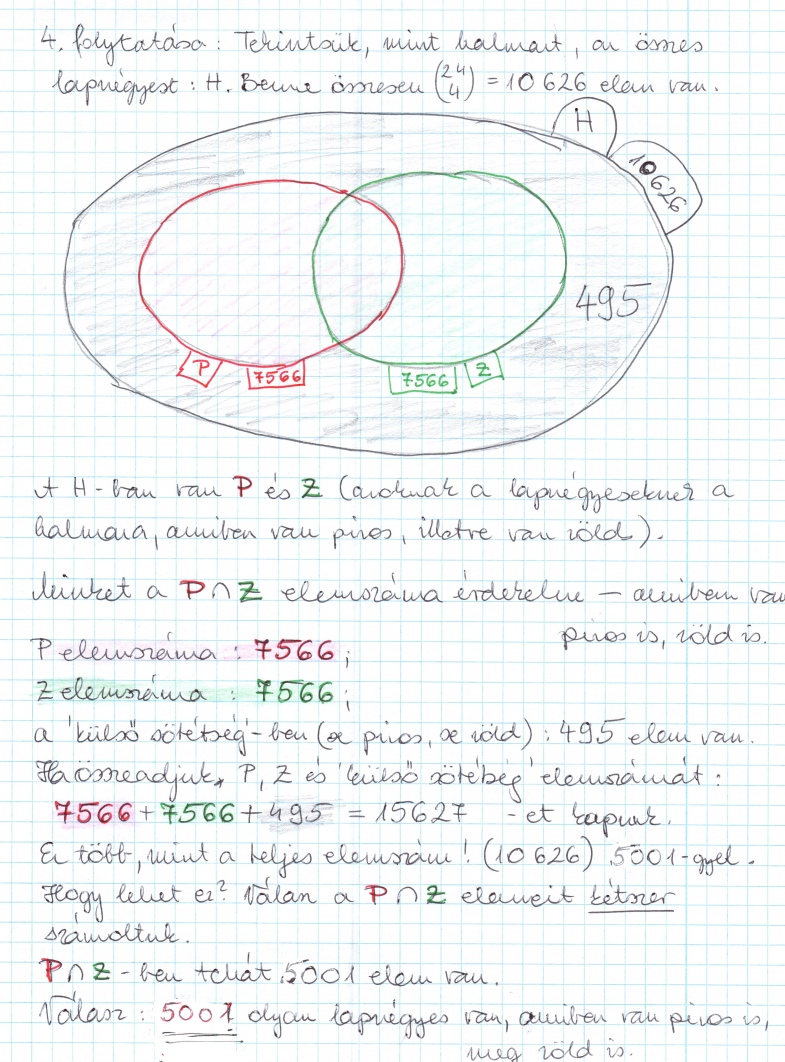
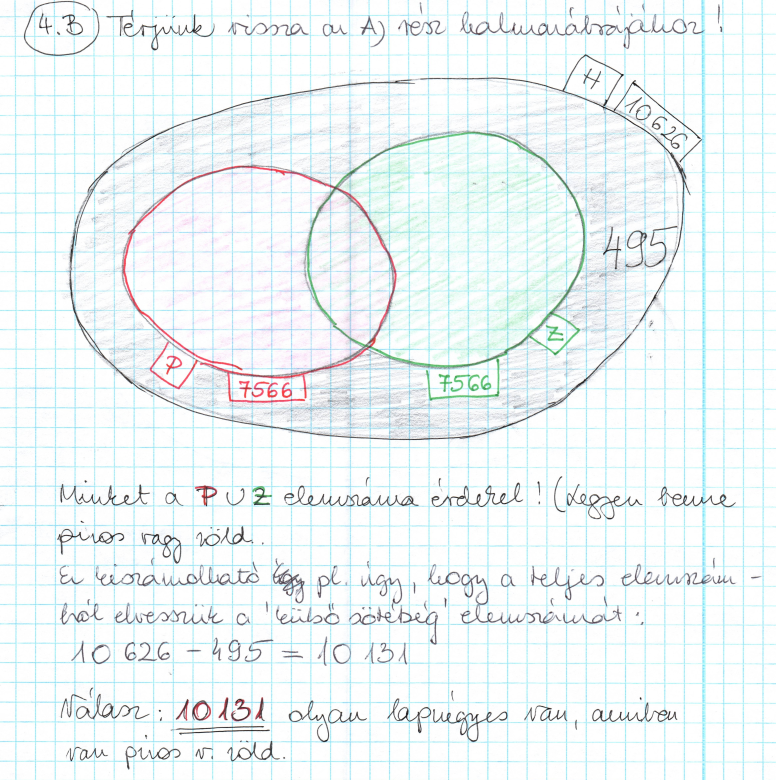
A) Hány olyan leosztás van, amelyben van piros is, és zöld is? (Mindkettõt szeretnénk.)
 
B) Hány olyan leosztás van, amiben van piros vagy zöld? (Nekünk mindkettõ jó, csak valamelyik legyen.)
 
C) Hány olyan osztás (lapnégyes) képzelhetõ el, amiben lesz nálunk piros is, meg ász is?