95. óra: Függvény értékkészlete

Például a félévi matematika-osztályzat egy függvény. Értelmezési tartománya a csoport tanulóinak halmaza, képhalmaza az \(\left\{1;2;3;4;5\right\}\) halmaz. Bár a képhalmaz minden eleme szóba jön, de ténylegesen csak a \(\left\{4;5\right\}\) halmaz elemeit vette fel értékként a függvény. Ilyenkor azt mondjuk, hogy a fv. értékkészlete: \[R_{\text{mat.jegy}}=\left\{4;5\right\}\]

Példa

Lineáris függvények esetén könnyen elõfordulhat, hogy az értelmezési tartomány nem a teljes valós  számhalmaz.

Tekintsük a \(g(x)=-\tfrac34x+\tfrac12\), \(x\in\left[-4;2\vphantom{\tfrac12}\right[\) függvényt! Adja meg a függvény értelmezési tartományát, grafikonját és értékkészletét!

A fv. értelmezési tartománya a megadott halmaz: \(\color{darkred}{D_g=\mathbf{\left[-4;2\vphantom{\tfrac12}\right[}}\)

A grafikon (a teli karika azt jelenti, hogy ott még 'él' a fv., az üres karika azt, hogy ott már épp' nincs fv.):

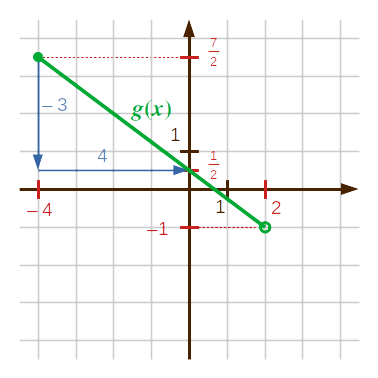
A függvény értékkészlete (a grafikon x-tengelyérõl leolvasva: \(\color{darkred}{R_g = \mathbf{\left]-1;\tfrac72\right]}}\).