91. óra: Lineáris függvény képlete

A lineáris függvény geometriai és algebrai értelemben is kevés adattal meghatározható. Mivel a grafikonja egyenes, azért pl. két pontja, vagy egy pontja és az irány már teljesen meghatározza. A feladat az, hogy a képletben szereplõ két együtthatót - a meredekséget (fõegyüttható) és a konstans tagot - meghatározzuk.

Két pontjával adott lineáris függvény képlete: Mi a képlete annak az \(f(x)\) lineáris fv.-nek, amelyrõl tudjuk, hogy
\[
f(-2) = -3\hphantom{00000}\text{és}\hphantom{00000}f(3)=7
\]

(1) Rajzoljuk be a grafikon két ismert pontját (kattintás az ábrán), majd a két ponton át a fv. grafikonját, mely egyenes (kattintás az ábrán)!   (2) A meredekség: A két ismert pont alapján megállapíthatjuk, hogy a grafikon 5 egységet elõre lépve 10-et emelkedik (kattintás).   Ha 5 egység alatt 10-et emelkedik, akkor 1 egység alatt \(\frac{10}5=2\) egységet kell emelkednie, tahát a grafikon meredeksége 2.   A függvény képletében ismerjük tehát a fõegyütthatót, így a függvény képlete: \[ f(x) = 2x + b\hphantom{00}\text{(ahol a }b\text{ konstans egyelõre ismeretlen)} \] (3) A konstans tag megállapítása: Helyettesítsük be az egyik ismert pontot a függvény (félig) ismert képletébe! Mondjuk legyen \(x=3\) \begin{equation} \begin{split} f(\color{darkgreen}{3}) &= 2\cdot\color{darkgreen}{3}+b\\ 7 &= 6+b\\ 1 &= b\hphantom{000}\text{Megvan a konstans tag!} \end{split} \end{equation}

A függvény képlete tehát:
\[
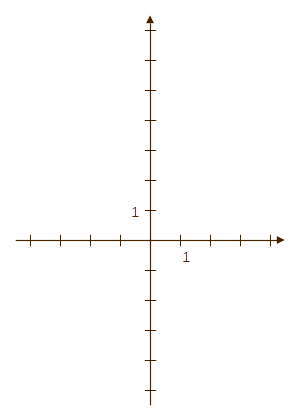\color{darkred}{\mathbf{f(x)=2x+1}}
\]

Egy pontjával és meredekségével adott lineáris függvény képlete: Mi a képlete annak az \(g(x)\) lineáris fv.-nek, amelyrõl tudjuk, hogy
\[
g(-2) = 7\hphantom{00000}\text{és}\hphantom{00000}\text{meredeksége: }-2
\]

(1) Rajzoljuk be a grafikon ismert pontját (kattintás az ábrán), majd a meredekség jelentését (kattintás)! (1 egység alatt -2-t 'emelkedik' a grafikon.)   Ezek alapján a \(g(x)\) függvény grafikonja megrajzolható (kattintás).   (2) A függvény képletében a fõegyütthatót (meredekség) már ismerjük, tehát a függvény képlete: \[ g(x) = -2x + b\hphantom{00}\text{(ahol a }b\text{ konstans egyelõre ismeretlen)} \] Helyettesítsük be az ismert pontot: \(x=-2\). \begin{equation} \begin{split} g(\color{darkgreen}{-2}) &= -2\cdot(\color{darkgreen}{-2})+b\\ 7 &= 4+b\\   3&= b\hphantom{000}\text{Megvan a konstans tag!} \end{split} \end{equation}

A függvény képlete tehát:
\[
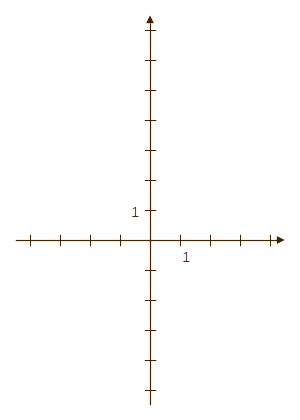\color{darkred}{\mathbf{g(x)=-2x+3}}
\]

Példa: Mi a képlete annak a \(h(x)\) lineáris függvénynek, melynek ismert két helyen az értéke:
\[
h(-4)=-1\hphantom{00000}\text{és}\hphantom{00000}h(2)=3
\]

(1) Rajzoljuk be a grafikon két ismert pontját (kattintás az ábrán)! Ezután a grafikont meg tudjuk rajzolni (kattintás) - hisz' tudjuk, hogy egyenes.   (2) A meredekség: A két ismert pont alapján a gra fikon 6 egység alatt 4-et emelkedik (kattintás az ábrán). Ha 6 egység alatt 4-et emelkedik, akkor 1 egység alatt a 4 hatod részét. Így a grafikon meredeksége: \[ \text{meredekség}=\frac46=\frac23 \] (3) A függvény képletében tehát a fõegyüttható \(\frac23\), a konstans (még) ismeretlen: \[ h(x)=\frac23x+c\hphantom{000}\text{a }c\text{ konstans még ismeretlen} \]Helyettesítsük be az egyik ismert pontot, mondjuk \(x=2\): \begin{equation} \begin{split} h(\color{darkgreen}{2}) &= \tfrac23\cdot\color{darkgreen}{2}+c\\ 3 &= \tfrac43 + c\\ 3-\tfrac43 &= c\\ \tfrac53 &= c\hphantom{00}\text{Megvan a konstans tag!} \end{split} \end{equation}

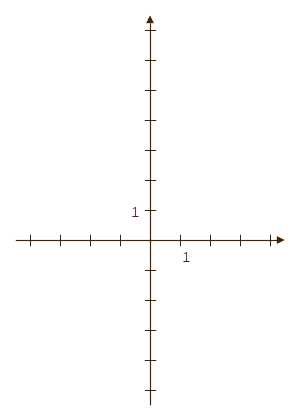A függvény képlete tehát:
\[
h(x) = \underline{\underline{\color{darkred}{\mathbf{\tfrac23x+\tfrac53}} }}
\]

Megjegyzés: A fenti példa azt próbálta bemutatni, hogy a keresett együtthatók nem mindig olyan 'szép' számok, hogy ránézésre láthatók legyenek, de a tanultakkal mégis pontosan kideríthetõk.