90. óra: Lineáris függvény ábrázolása

A lineáris függvény ismertetõjele grafikailag az, hogy a fv. grafikonja egyenes (v. szakasz v. félegyenes). Algebrai ismertetõjegye az, hogy  a lineáris fv. képlete legfeljebb elsõfokú polinom. \(\left(f(x)=ax+b\right.)\)

 

A képlet együtthatóinak geometriai jelentése

A lineáris függvény képletében \(\left(f(x)=ax+b\right.)\) két rögzített (valós) együttható van:

A függvény grafikonjára nézve mindkettõnek pontos jelentése van.

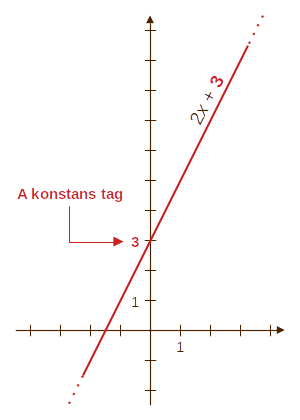
A konstans tag jelentése: Ha a függvény képlete pl. \(f(x)=2x+3\), akkor \(x\) helyére nullát írva pont 3-at, vagyis a konstans tag értékét kapjuk:
\[
f(0) = 2\cdot0+3=\color{darkred}{\mathbf{3}}
\](És ez mindig így van, hiszen \(x=0\) mellet a fõtag nullává válik.)
 
A konstans tag jelentése tehát a fv. nullában felvett értéke:
 
a grafikon ott metszi az y-tengelyt.

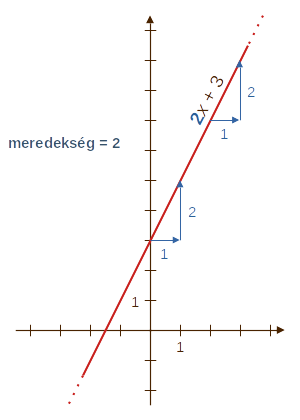
A fõegyüttható jelentése: Ha a függvény képlete pl. \(f(x)=2x+3\), akkor \(x\) helyére eggyel többet írva a fv. értéke annyival nõ, amennyi a fõegyüttható \((a)\).
\[
f(x+1) = 2(x+1)+3 = 2x+1+3=2x+3+1=\color{darkred}{\mathbf{f(x)+2}}
\]És ez mindig így van:
\[
f(x+1) = a(x+1)+b = ax+a+b=\color{darkred}{ax+b}+a=\color{darkred}{\mathbf{f(x)+a}}
\]
 
A fõegyüttható jelentése tehát az, hogy ha az x-tengely irányába (bárhol is) egyet elõre lépünk, akkor mennyivel nõ a fv. értéke:
 
a grafikon egy egység alatt ennyit 'emelkedik'.
 
Ez a szám (a fõegyüttható) valahogy azt fejezi ki milyen erõsen emelkedik a grafikon. Ezért a másik neve:
 
a grafikon meredeksége.

 

Példa: Ábrázoljuk a \(g(x)=3x-2\), \(x\in\mathbb R\) függvényt!

(1) A konstans tag \(-2\), tehát a grafikon a \(-2\)-nél metszi az y-tengelyt. (Kattintás az ábrán.)
 
(2) A függvény meredeksége \(3\), tehát a várt grafikon 1 egység alatt 3-at fog emelkedni (kattintás az ábrán).
 
(3) A fv. grafokonja így már meghúzható - hisz' tudjuk, hogy egyenes. (Kattinitson az ábrán!)
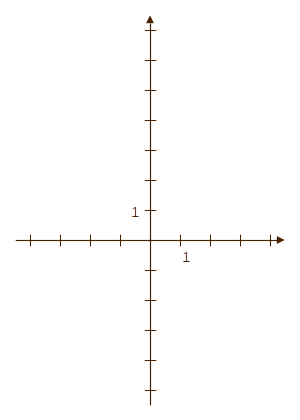