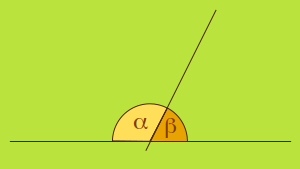
I. mellékszögek: Két szöget mellékszögnek mondunk, ha csúcsuk azonos, egyik száruk közös, másik pedig egymás folytatása.   Állítás: Mellékszögek összege 180°. (α + β = 180°.)   Indoklás: Ketten egymás mellett kiadják az egyenesszöget, ami 180°.

Értelmezés: Ha két szög összege 180°, akkor azt mondjuk, hogy õk kiegészítõ szögek.
 
Megjegyzés: A kiegészítõ szögek nem feltétlenül mellékszögek - lehet, hogy más a kölcsönös helyzetük; de a mellékszögek biztosan kiegészítõ szögek.

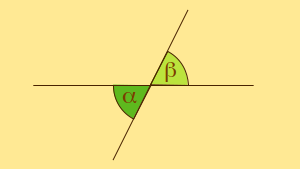
II. csúcsszögek: Két metszõ egyenes metszéspontjában álló átellenes két szög (mint szögpár).   Állítás: Csúcsszögek egyenlõk. (α = β.)   Indoklás (1) Rajzoljuk meg azt a δ szöget, amely mindkettõnek mellékszöge! (Kattintson az ábrán!)

 
(2) Ez a \(\delta\) mindkét szögnek (α és β) kiegészítõ szöge, így
\begin{equation}
\begin{split}
\alpha + \delta &= 180^\circ\\
\beta + \delta &= 180^\circ\\
\text{Rendezve:}\\
\alpha &= 180^\circ - \delta\\
\beta &= 180^\circ - \delta
\end{split}
\end{equation}Vagyis α = β. és ezt akartuk bizonyítani.

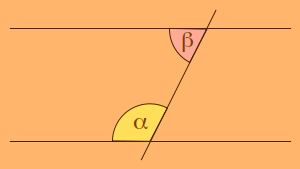
III. társszögek: Ha két párhuzamos egyenest metsz egy harmadik, akkor az egy oldalon fekvõ belsõ szögeket társszögeknek nevezzük.   Állítás: Társszögek összege 180°. (α + β = 180°.) (Vagyis a társszögek kiegészítõ szögek.)   Indoklás: Abból indulunk ki, hogy a párhuzamosok nem metszhetik egymást.

(1) Ha α + β < 180°. volna, akkor a párhuzamossági axióma szerint (Euklidesz V. axiómája) a két párhuzamos egyenes metszené egymást azon az oldalon, ahol α és β vannak. (Kattintson az ábrán!)
Ez ellentmondás (párhuzamosok nem metszhetik egymást). Így α + β < 180° nem lehetséges.
 
(2) Ha α + β > 180°. volna, akkor α és β mellékszögeinek összege lenne kisebb  180°-nál. (Kattintás az ábrán.)
(Magyarázat: a két mellékszögpár teljes összege 2 · 180° = 360°, így ha α + β > 180°, akkor a két mellékszög összege < 180°.)
Ekkor a párhuzamossági axióma szerint a két párhuzamos egyenes metszené egymást azon az oldalon, ahol α és β mellékszögei vannak. (Kattintson az ábrán!) Eszerint α + β > 180° sem lehetséges.
 
(3) Marad tehát, hogy α + β = 180° és ezt akartuk igazolni.

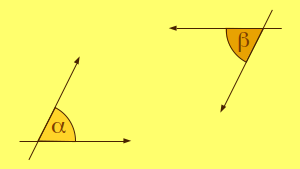
IV. váltószögek: Két szöget váltószögnek mondunk, ha száraik párhuzamosak és ellentétes irányításúak.   Állítás: Váltószögek egyenlõk. (α = β.)   Indoklás: (1) Hosszabítsuk meg a két szög (α és β) egy-egy nem párhuzamos szárát metszésig! (Kattintson az ábrán!) (2) A metszéspontnál kialakul egy δ szög, mely mindkét eredeti szögnek társszöge. (Kattintson az ábrára!)

 
(3) Így a társszögekrõl elõbb igazoltak szerint:
α + δ = 180°
β + δ = 180°,
azaz
α = 180° - δ
β = 180° - δ
tehát α = β. És ezt akartuk bizonyítani.

V. egyállású szögek: Két szöget egyállásúnak mondunk, ha száraik párhuzamosak és egyezõ irányításúak.   Állítás: Egyállású szögek egyenlõk. (α = β.)   Indoklás: (1) Hosszabítsuk meg az egyik szög (mondjuk β) szárait a csúcson túl! (Kattintson az ábrán!) (2) Kialakul egy δ szög, mely csúcsszöge β-nak. (Kattintson az ábrára!)

 
(3) A csúcsszögekrõl igazoltak szerint: δ = β. Ugyanakkor ez a δ váltószöge α-nak, így α = δ.
Összefoglalva: α = δ = β.
Azaz α = β. (Euklidesz ezt úgy mondta: 'Ha két mennyiség egy harmadikkal egyenlõ, akkor a két mennyiség egymással is egyenlõ.')