5. óra: Halmazmûveletek

A mûvelet - hasonlóan a számokhoz - valami olyan hozzárendelési szabály, ami két objektumból egy harmadikat 'csinál'. Pl. két szám összege, vagy szorzata egy harmadik. Ezek a kétváltozós mûveletek. Vannak egyváltozós mûveletek is, amelyek egy számból egy másikat 'csinálnak'. Pl. a négyzetgyök.

Halmazok esetében is hasonló a helyzet, a kétváltozós mûveletek két halmazból egy harmadikat 'gyártanak', az egyváltozós mûveletek egy halmazból egy másikat.

Fussuk át a legfontosabbakat!

 

Metszet

Értelmezés: Az \(A\) és \(B\) halmazok metszete (közös része) azokból az elemekbõl áll, amelyek mindkét halmazban megvannak. (Kattintás az ábrán!)
Matematikai jelöléssel:
\[
A\cap B :=\left\{x\,\big|\,x\in A\text{ és }x\in B\right\}
\]
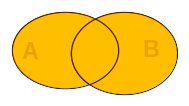Két halmaz metszete (katt.!)
Megjegyzés: Ha két halmaz metszete üres (nincs közös elemük),
akkor azt mondjuk, hogy a két halmaz diszjunkt.

1. példa: Legyen \(A\) a 2-vel osztható számok halmaza, \(B\) pedig a 3-mal osztható számok halmaza.
Ekkor \(A\cap B\) a 6-tal osztható számok halmaza lesz. (Ezek azok a számok, amik 2-vel és 3-mal is oszthatók.)

2. példa: Legyen \(C=[-1;2]\) és \(D=]1;7[\).
Ekkor \(C\cap D = ]1;2]\).

 

Unió

Értelmezés: Az \(A\) és \(B\) halmazok uniója (egyesítése) azokból az elemekbõl áll, amelyek valamelyik halmazban megvannak. (Kattintás az ábrán!)
Matematikai jelöléssel:
\[
A\cup B :=\left\{x\,\big|\,x\in A\text{ vagy }x\in B\right\}
\]
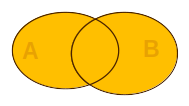Két halmaz uniója (katt.!)

1. példa: Legyen \(A\) a 9.A tanulóniak halmaza, \(B\) pedig a 9.B tanulóinak halmaza.
Ekkor \(A\cup B\) a 9. évfolyam diákjainak halmaza lesz.

2. példa: Legyen \(C=[-1;2]\) és \(D=]1;7[\).
Ekkor \(C\cup D = [-1;7[\).

 

Kivonás, vagy különbségképzés

Értelmezés: Ha az \(A\) halmazból kivonjuk a \(B\) halmazt, az eredményhalmaz \(A\)-nak azokat az elemeit tartamlazza, amelyek nincsenek a \(B\)-ben. (Kattintás az ábrán!)
Matematikai jelöléssel:
\[
A\setminus B :=\left\{x\in A\,\big|\,x\notin B\right\}
\]
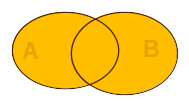Az \(A\) mínusz \(B\) halmaz (katt.!)

1. példa: Legyen \(A\) a 2-vel osztható számok halmaza, \(B\) pedig a 3-mal osztható számok halmaza.
Ekkor \(A\setminus B\) a 6-tal nem osztható osztható páros számok halmaza lesz. (Ezek azok a számok, amik 2-vel oszthatók, de 3-mal nem.)

2. példa: Legyen \(C=[-1;2]\) és \(D=]1;7[\).
Ekkor \(C\cap D = [-1;1]\).