
4. óra: Részhalmazok I.
| Értelmezés:
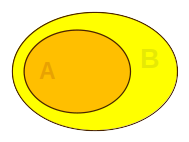
Azt mondjuk, hogy az \(A\) halmaz része (v. részhalmaza)
a \(B\) halmaznak, ha \(A\) minden eleme egyben a \(B\)-nek is
eleme. Jele: \(A\subset B\). |
 |
Az üreshalmaz (jele: \(\emptyset\) pedig minden halmaznak részhalmaza. (Hiszen az üreshalmaz minden eleme - egy sincs neki - egyben eleme a tetszõlegesen választott \(H\) halmaznak is.
Ezt a két szélsõséges részhalmazt triviális részhalmaznak nevezzük.
Például a 9.A német haladó csoportja részhalmaza a 9.A osztálynak.
Vagy pl. a múlt órákon tanult nevezetes számhalmazok között fennállnak
az alábbi tartalmazási relációk:
\[
\mathbb N \subset\mathbb Z\subset\mathbb Q\subset\mathbb R
\]Az irracionális számok \(\mathbb Q^*\) halmaza ebbõl egy kicsit kilóg,
\(\mathbb Q^*\subset \mathbb R\), de a többiekhez semmi köze.
Részhalmazok megadása tulajdonsággal
Ha egy részhalmazt meg akarunk adni, a legjobb eljárás, ha megnevezzük
a halmazt (amelynek részét kívánjuk) és megadjuk azt a tulajdonságot,
amely kijelöli a részhalmazba felvenni kívánt elemeket.
Ennek matematikai jelekkel való leírása (itt \(H\) egy halmaz, \(T(x)\)
pedig egy azonértelmezett tuljdonság):
\[
\left\{x\in H\,\big|\,T(x)\right\}
\]Olvasata: ,,azon x elemek a H-ból, melyek rendelkeznek a T(x)
tulajdonsággal.''
Megjegyzés: A ,,\(\big|\)''
helyett a kettõspont is használható.
Példák
1. A pozitív számok halmaza: \(A=\left\{x\in\mathbb R\,\big|\,x>0\right\}\);
2. A hárommal osztható egész számok halmaza:
\(B=\left\{n\in\mathbb Z\,:\,3\mid n\right\}\);
(Itt azért használtunk kettõspontot, mert
a függõleges vonalat az oszthatóság jelére tartjuk fenn.)
3. Az irracionális számok egy ilyen módon történõ leírása: \(\mathbb Q^*=\left\{x\in\mathbb R\,\big|\,x\notin\mathbb Q\right\}\);
Intervallumok
Ezekre külön jelöléseket vezettek be a matematikában.
Nézzük!
Szakasz-jellegû intervallumok
Megnevezzük a szakasz alsó és felsõ végpontját, és jelöléssel tudatjuk, hogy a végpontok közül melyik tartozik hozzá az intervallumhoz. (A jelölésben mindig az alsó határ áll elöl.)
Zárt intervallum: Mindkét végpont az intervallumhoz
tartozik. Pl.: \(\left[2;5\right]\). Olv.: ,,kettõ-öt zárt
intervallum''.
Halmazelméleti jelekkel: \(\left[2;5\right] = \left\{x\in\mathbb
R\,\big|\,2\le x\le5\right\}\)
Rajzban: 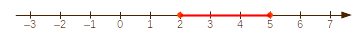 (A szakasz két végét
'teli pötty' zárja le.)
(A szakasz két végét
'teli pötty' zárja le.)
Nyílt intervallum: Egyik végpont sem tartozik az
intervallumhoz. Pl.: \(\left]-1;3\right[\) vagy \(\left(-1;3\right)\).
Olv.: ,,mínusz egy-három nyílt intervallum''.
Halmazelméleti jelekkel: \(\left]-1;3\right[ = \left\{x\in\mathbb
R\,\big|\,-1< x<3\right\}\)
Rajzban: 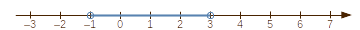 (A szakasz két végét 'üres
karika' zárja le.)
(A szakasz két végét 'üres
karika' zárja le.)
Balról zárt, jobbról nyílt intervallum: Az alsó (bal)
végpont az intervallumhoz tartozik, a felsõ (jobb) végpont nem. Pl.:
\(\left[\frac12;4\right[\) vagy \(\left[\frac12;4\right)\). Olv.: ,,egyketted-négy
balról zárt, jobbról nyílt intervallum''.
Halmazelméleti jelekkel: \(\left[\frac12;4\right) = \left\{x\in\mathbb
R\,\big|\,\frac12\le x<4\right\}\)
Rajzban: 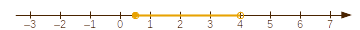 (Bal végét
'teli', jobb végét 'üres karika' zárja le.)
(Bal végét
'teli', jobb végét 'üres karika' zárja le.)
Balról nyílt, jobbról zárt intervallum: Az alsó (bal)
végpont nem tartozik az intervallumhoz, a felsõ (jobb) végpont viszont
igen. Pl.: \(\left]-2;1{,}5\right]\) vagy \(\left(-2;1{,}5\right]\).
Olv.: ,,mínusz kettõ-másfél balról nyílt, jobbról zárt
intervallum''.
Halmazelméleti jelekkel: \(\left]-2;1{,}5\right] = \left\{x\in\mathbb
R\,\big|\,-2< x\le 1{,}5\right\}\)
Rajzban: 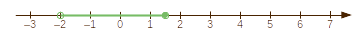 (Bal végét
'üres', jobb végét 'teli karika' zárja le.)
(Bal végét
'üres', jobb végét 'teli karika' zárja le.)
Félegyenes jellegû intervallumok
Az ilyen intervallum egyik vége egy valós szám, a másik csak egy irány, melyet a '\(\infty\)' vagy a '\(-\infty\)' szimbólum jelöl. Ezek a szimbólumok nem valós számok, ezért õket sohasem vehetjük hozzá az intervallumhoz. (A félegyenes szimbólum felõli vége mindig nyílt!)
Példák:
A 2-nél nagyobb számok halmaza: \(\left[2;\infty\right[\) vagy \(\left[2;\infty\right) = \left\{x\in\mathbb R\,\big|\,2\le x\right\}\)
A 2-nél kisebb számok halmaza: \(\left]-\infty;2\right[\) vagy \(\left(-\infty;2\right) = \left\{x\in\mathbb R\,\big|\,x<2\right\}\)
Stb.
