3. óra: Számhalmazok (folyt,)

Az elõzõ óráról maradt még egy adósságunk...

Az állítást azzal indokoljuk, hogy mutatunk egy módszert (egy konkrét számra), ami egy végtelen szakaszos tizedes törtet közönséges törtté alakít (azaz két egész szám hányadosává.

A példánk az \(x=0{,}81818181\ldots=0{,}\dot{8}\dot{1}\) lesz.

1. lépés: Mivel a szakasz kettõ-hosszú, azért ha 100-zal beszorozzuk a számot, a szakaszok önmagukon belül, de azonos pozícióba tolódnak el: \(100x=81{,}81818181\ldots=81{,}\dot{8}\dot{1}\)

2. lépés: Írjuk egymás alá a két összefüggést!
\begin{equation}
\begin{split}
100x &= 81{,}81818181\ldots &=81{,}\dot{8}\dot{1}\\
x &= 0{,}81818181\ldots&=0{,}\dot{8}\dot{1}
\end{split}
\end{equation}

Ha a két egyenletet kivonjuk egymásból, kapjuk, hogy
\[
99x = 81
\]Ezt rendezve: \(x\frac{81}{99}\), amit még egyszerûsítünk 9-cel (mert lehet). Így kapjuk, hogy \(x=\frac9{11}\).

Eredményünk:
\[
x = 0{,}81818181\ldots=0{,}\dot{8}\dot{1} = \frac9{11}
\]Tehát sikerült!

Ellenõrizzük le az eredményt!
\[
\begin{array}{cccccccccccc}
9&:&1&1&=&0&,&8&1&8&1&\ldots\\
9&0&&&&&&&&&&\\
&2&0&&&&&&&&&\\
&&9&0&&&&&&&&\\
&&&2&0&&&&&&&\\
&&&&9&..&&&&&&
\end{array}
\]Minden rendben!

 

Folytassuk a számhalmazok felsorolását!

Eddig voltak a természetes számok \((\mathbb N)\), az egész számok \((\mathbb Z)\) és a racionális számok \((\mathbb Q)\).

A racionális számok nem minden, mert kimaradta a végtelen, de nem szakaszos tizedes törtek. Azokat irracionális számoknak nevezzük. Az irracionális számok tehát azok, amelyek nem írhatók fel két egész szám hányadosaként. A halmaz jele: \(\mathbb Q^*\).

A racionális és irracionális számok együtt alkotják a valós számok halmazát. Jele: \(mathbb R\).
A valós számok tehát azok, amelyek a számegyenesen agyáltalán elõfordulnak.

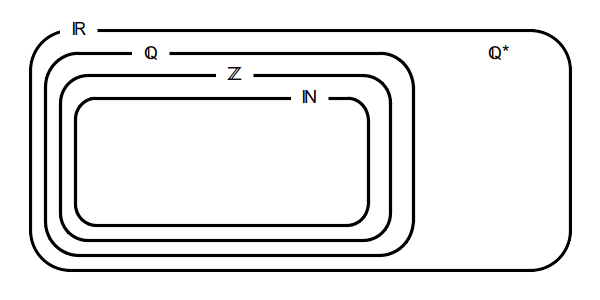
A számhalmazok egymáshoz való viszonyát fejezi ki az alábbi ábra: