Harasztos Barnabás lapja

Processing math: 100%

Mintadolgozatok

I. feladatsor

I.1. feladat: Oldja meg a valós számok halmazán az alábbi egyenletet:

$3^{x^2}= 27\cdot 9^x$ (Vigyázzanak!

$3^{x^2}\ne\left(3^x\right)^2$ .)

Megoldás (fenn van): (megjelenik) ↓ (eltûnik) ↑

I.2. feladat: Oldja meg a valós számok halmazán az alábbi egyenlõtlenséget:

$\log_2(x^2-5x+8) \le 1$

Megoldás (fenn van): (megjelenik) ↓ (eltûnik) ↑

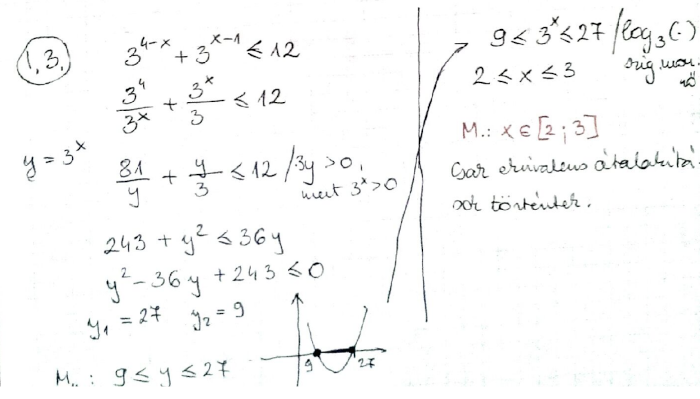
I.3. feladat: Oldja meg a valós számok halmazán az alábbi egyenlõtlenséget:

$3^{4-x} + 3^{x-1} \le 12$

Megoldás (fenn van): (megjelenik) ↓ (eltûnik) ↑

I.4. feladat: Oldja meg a valós számok halmazán az alábbi egyenletet:

$\log_x 8 - \log_{4x} 8 = \log_{2x} 16$

Megoldás (fenn van): (megjelenik) ↓ (eltûnik) ↑

I.5. feladat: Oldja meg a valós számok halmazán az alábbi egyenletet:

$(2x+1)^{\text{lg}(2x+1)-3} = 0{,}01$

Megoldás (fenn van): (megjelenik) ↓ (eltûnik) ↑

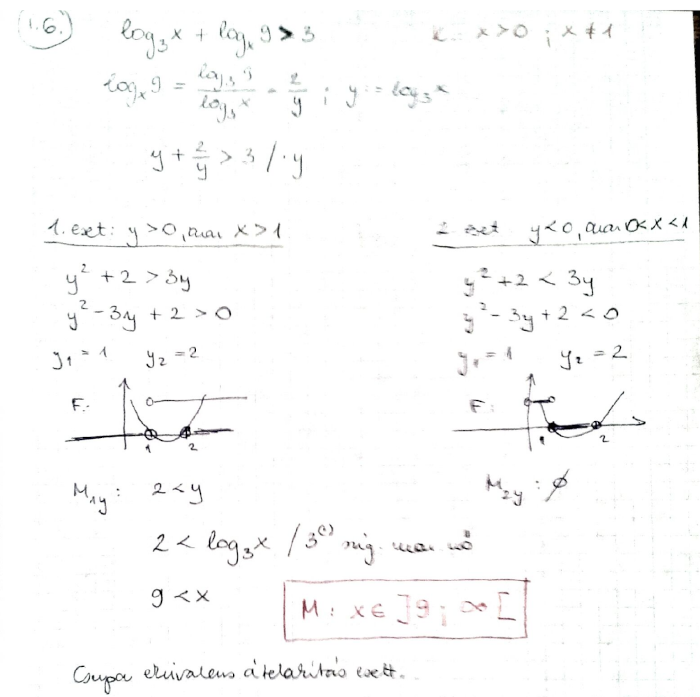
I.6. feladat: Oldja meg a valós számok halmazán az alábbi egyenlõtlenséget:

$\log_3 x + \log_x 9 > 3$

Megoldás (fenn van): (megjelenik) ↓ (eltûnik) ↑

II. feladatsor

II.1. feladat: Oldja meg a valós számok halmazán az alábbi egyenletet:

$5\cdot 2^{2x+1} - 4^{x+1} + 3\cdot 4^x = 6\cdot 4^{x-1} + 15$

Eredmény (fenn van): (megjelenik) ↓ (eltûnik) ↑

$\color{darkred}{\mathbf{x=\frac12}}$

II.2. feladat: Oldja meg a valós számok halmazán az alábbi egyenlõtlenséget:

$\log_{\frac34}(4x-5)\ge \tfrac9{16}$

Eredmény (fenn van): (megjelenik) ↓ (eltûnik) ↑

$\color{darkred}{\mathbf{x\in\left]\frac54;\frac74\right]}}$

II.3. feladat: Oldja meg a valós számok halmazán az alábbi egyenlõtlenséget:

$\left(\frac12\right)^{\sqrt{x}}>0{,}25$

Eredmény (fenn van): (megjelenik) ↓ (eltûnik) ↑

II.4. feladat: Oldja meg a valós számok halmazán az alábbi egyenletet:

$\log_5(x+1) + \log_5(x-1) = \log_5 8 + \log_5(x-2)$

Eredmény (fenn van): (megjelenik) ↓ (eltûnik) ↑

$\color{darkred}{\mathbf{x_1=3}}\hphantom{000000000} \color{darkred}{\mathbf{x_2=5}}$

II.5. feladat: Oldja meg a valós számok halmazán az alábbi egyenlõtlenséget:

$\log_{\frac1{x^2}}(x^2-2x-8)\ge 0$

Eredmény (fenn van): (megjelenik) ↓ (eltûnik) ↑

$\color{darkred}{\mathbf{x\in\left[1-\sqrt{10};-2\vphantom{1^1_1}\right[\cup\left]4;1+\sqrt{10}\vphantom{1^1_1}\right]}}$ vagy közelítõ értékkel:

$\color{darkred}{\mathbf{x\in\left[-2{,}162;-2\vphantom{1^1_1}\right[\cup\left]4;4{,}162 \vphantom{1^1_1}\right]}}$

II.6. feladat: Oldja meg a valós számok halmazán az alábbi egyenletrendszert:

$\left. \begin{array}{rcl} \log_8 x + \log_4 y^2 &=& 5\\ \log_8 y + \log_4 x^2 &=& 7\\\hline \end{array} \right\}$

Eredmény (fenn van): (megjelenik) ↓ (eltûnik) ↑

$\color{darkred}{\mathbf{x=64}}\hphantom{000000000} \color{darkred}{\mathbf{y=8}}$