Harasztos Barnabás lapja

93. óra: Az integrál

A függvény és a derivált közti szoros kapcsolat miatt nem csak az lehet érdekes, hogy mi egy $f(x)$ függvény deriváltja, hanem az is, hogy kinek a deriváltja az $f(x)$ ?

Definíció: Azt az

$F(x)$ függvényt, amelynek az

$f(x)$ a deriváltja:

$F'(x)=f(x)$ az

$z(x)$ primitív függvényének, vagy határozatlan integráljának nevezzük. Jele:

$F(x) = \int f(x) \mbox{ d}x$

A deriválás és az integrálás közti kapcsolat kissé emlékeztet a szorzás/osztás köztire. (Egyik oda, másik vissza.)
Az analógia annyiban is fennáll, hogy deriválni általában könnyebb (legalábbis viszonylag), mint integrálni.

A határozatlan integrál - mivel a konstans fv. deriváltja zérus - egy additív (hozzáadódó) konstans erejéig határozatlan.

Plédául:
$\int x^2 \text{ d}x = \frac{x^3}3 + c\text{, ahol }c\in\mathbb R$ A $c$ additív konstans odaírásával azt fejezzük ki, hogy ott bármilyen szám állhat - azt nem ismerjük.

Ha egy kicsit kevésbé szertnénk határozatlanok lenni, elõírhatjuk, hogy azon függvények közül, melyek deriváltja $f(x)$ , nekünk melyik kell. Célszerûen a választékból azt szoktuk elõírni, hogy hol legyen a zérushelye:

Legyen az

$f:D_f\rightarrow\mathbb R$ fv. értelmezési tartományának egy kitüntetett eleme

$a\in D_f$ .

Definíció: Azt az

$F(x)$ függvényt, amely...

$\bullet$ egyrészt primitív függvénye az

$f(x)$ -nek:

$F'(x)=f(x)$ ,

$\bullet$ másrészt a kitüntetet

$a\in D_f$ helyen zérust vesz fel:

$F(a)=0$ ,
az

$f(x)$ függvény $a$ -ban eltûnõ integrálfüggvényének nevezzük.
Jele:

$F(x) = \int\limits_a f(x)\mbox{ d}x$

Ez már egyértelmûsíti a függvényt. Például az $f(x)=2x$ függvény határozatlan integrálja:
$\int 2x\mbox{ d}x = x^2+c$ Ha azonban a nullában eltûnõ integrálfüggvényt keressük, abból csak egy van:
$\int\limits_0 2x\mbox{ d}x = x^2$ Ugyanennek a $2x$ -nek mondjuk a 3-ban eltûnõ intergálfüggvénye:
$\int\limits_3 2x\mbox{ d}x = x^2-9$ Stb.

Mire jó ez?

Egy fontos tétel következik. Elõször a szemléletesség (jobb érthetõség) kedvéért kissé pontatlanul kimondva.

Tekintsünk egy

$f(x)$ folytonos valós függvényt, s a függvény értelmezési tartományában egy

$a\in D_f$ pontot!
Jelölje

$T(x)$ a függvény görbéje alatti területet a rögzített

$a$ és a változó

$x\in D_f$ között!
(Ahogy

$x$ változik, vele változik a

$T$ is, így

$T$ az

$x$ függvénye.)

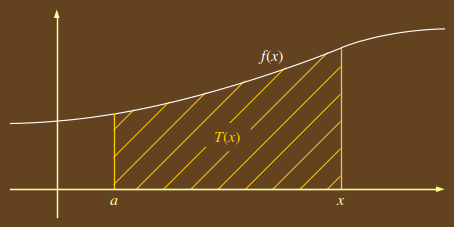
(Hallgatólagosan feltételezzük, hogy a terület mindig létezik.)

Newton‒Leibniz-tétel: A

$T(x)$ függvény az

$f(x)$ fv.

$a$ -ban eltûnõ integrálfüggvénye:

$T(x) = \int\limits_a f(x)\mbox{ d}x$

Bizonyítás

Az, hogy

$T(x)$ az

$a$ -ban eltûnik, vagyis

$T(a)=0$ elég jól látszik. Ilyenkor a terület egy szakasszá zsugorodik, melynek területe zérus.

Nehezebb annak igazolása, hogy

$T'(x) = f(x)$ . Vizsgálnunk kell a

$\lim_{\Delta x\rightarrow0}\frac{T(x+\Delta x)-T(x)}{\Delta x}$ határértéket.

Az egész bizonyítás a rendõr-elven alapszik. Meg kell becsülnünk mindkét irányból a

$T(x+\Delta x)-T(x)$ -et.

1. eset:

$f(x)>0$ és az

$x$ környezetében monoton növõ

Legyen elõször

$\Delta x>0$ , vagyis vizsgáljuk a jobboldali határértéket!

(1) Menjünk odébb

$\Delta x$ -nyivel! (Kattintás az ábrán!)

(2) Az addig terjedõ terület a

$T$ definíciója szerint

$T(x+\Delta x)$ , így a

$T(x+\Delta x)-T(x)$ az ábrán jelzett sûrûbben vonalkázott terület. (Katt.!)

(3) E terület nagyobb-egyenlõ, mint a beírt,

$f(x)$ magasságú téglalapé (katt!). Így fennáll:

$f(x)\cdot\Delta x \le T(x+\Delta x)-T(x)$

(4) A

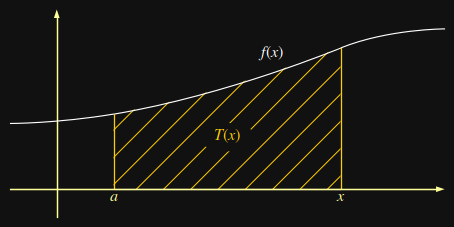$T(x+\Delta x)-T(x)$ terület viszont kisebb-egyenlõ, mint a körülírt,

$f(x+\Delta x)$ magasságú téglalapé (kattintás). Így fennál a felsõ becslés is:

$T(x+\Delta x)-T(x) \le f(x+\Delta x)\cdot\Delta x$

Összefoglalva: ha

$f(x)>0$ , az

$x$ valamely környezetében monoton növõ, és

$\Delta x>0$ , akkor:

$\begin{equation} \begin{split} f(x)\cdot\Delta x &\le T(x+\Delta x)-T(x) \le f(x+\Delta x)\cdot\Delta x\\\\ f(x) &\le \frac{T(x+\Delta x)-T(x)}{\Delta x} \le f(x+\Delta x) \end{split} \end{equation}$ Ha most

$\Delta x \rightarrow+0$ akkor az

$f(x)$ függvény folytonossága alapján mindkét szélen

$f(x)$ -hez tartó kifejezés áll, így a rendõr-elv alapján a közrefogott tag is oda tart. Amit mondhatunk:

$\lim_{\Delta x\rightarrow +0}\frac{T(x+\Delta x)-T(x)}{\Delta x} = f(x)$

Ha most

$\Delta x<0$ , akkor az ábrát erõsen figyelve megállapíthatjuk, hogy a becslés most is megáll, csak éppen fordítva (a sok mínusz jel azt hivatott kezelni, hogy a területek pozitívnak jöjjenek ki):

$\begin{equation} \begin{split} f(x)\cdot\left(-\Delta x\right) &\ge -\left[\vphantom{1^1_1}T(x+\Delta x)-T(x)\right] \ge f(x+\Delta x)\cdot\left(-\Delta x\right)\\\\ f(x)\cdot\Delta x &\le \vphantom{1^1_1}T(x+\Delta x)-T(x) \le f(x+\Delta x)\cdot\Delta x\\\\ f(x) &\ge \frac{T(x+\Delta x)-T(x)}{\Delta x} \ge f(x+\Delta x) \end{split} \end{equation}$ De a rendõr-elvnek így is jó. Most azt mondhatjuk, hogy

$\lim_{\Delta x\rightarrow -0}\frac{T(x+\Delta x)-T(x)}{\Delta x} = f(x)$
Ha a jobb és a bal oldali határérték megegyezik, akkor az a határérték:

$\lim_{\Delta x\rightarrow 0}\frac{T(x+\Delta x)-T(x)}{\Delta x} = f(x)$
Vagyis

$T'(x) = f(x)$
Ezzel kész is volnánk...
...de van még egy pár eset.

2. eset: Mi van, ha

$f(x)>0$ , és az

$x$ egy környezetében monoton fogyó?

Nincs azzal semmi baj, csak akkor minden becslésünk megfordul... hagyjuk!

3. eset:

$f(x)>0$ , és éppen ott van a fv.-nek maximuma, vagy minimuma - még egy ici-pici környezetben sem monoton. Ekkor is megy minden, csak a jobb és baloldali becsléseink egy irányból igazolják e tételt...

Az igazi baj az, ha

$f(x)<0$ . Akkor bizony minden borul, mert a terület (ami nem nagyon szeret negatív lenni) nem becsülhetõ olyan negatív dolgokkal, mint

$f(x)$ vagy efféle.

Mi legyen hát?

Newton megoldása a következõ:

$T(x)$ jelentése NE a szokásos terület, hanem ún. elõjeles terület legyen!
Ez pontosan azt jelentse, hogy az x-tengely alatti területek negatívnak számítsanak! Ha így teszünk, nemcsak a bizonyításaink lesznek rendben, de a fizika is szépen ezzel vág egybe. (Ezért is oldotta meg így Newton.)

Érdekes tapasztalataink alapján újrafogalmazzuk a tételt (most már pontosabban).

Tekintsünk egy

$f(x)$ folytonos valós függvényt, s a függvény értelmezési tartományában egy

$a\in D_f$ pontot!
Jelölje

$T(x)$ a függvény grafikonja és az x-tengely közé esõ elõjeles területet a rögzített

$a$ és a változó

$x\in D_f$ között!
Az elõjeles terület azt jelenti, hogy az x-tengely fölött lévõ terület pozitívnak számít, az x-tengely alatti terület negatívnak számít. (Titkon akkor is negatívnak számít a

$T(x)$ , ha az

$x$ az

$a$ alá kerül.)

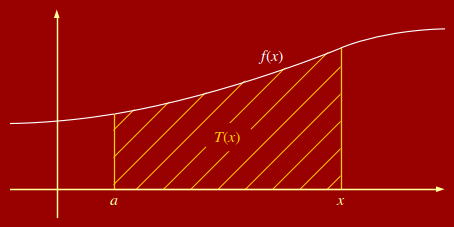
(Hallgatólagosan feltételezzük, hogy a terület az

$f(x)$ görbéje és az x-tengely között mindig létezik.)

Newton‒Leibniz-tétel: A

$T(x)$ függvény az

$f(x)$ fv.

$a$ -ban eltûnõ integrálfüggvénye:

$T(x) = \int\limits_a f(x)\mbox{ d}x$

Vegyük használatba az új tudásunkat!

Példák

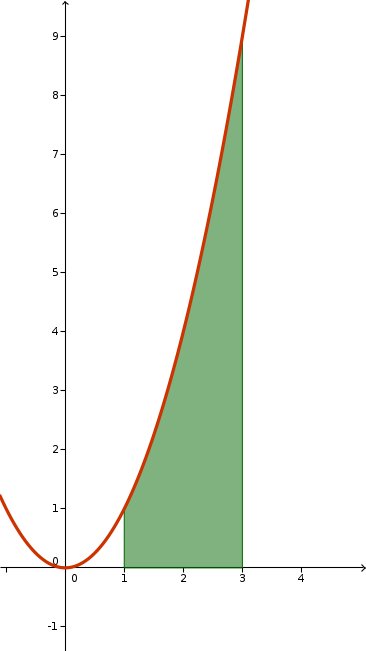
1. példa

Határozzuk meg a

$g(x)=x^2$ függvény görbéjének az

$x=1$ és az

$x=3$ közé esõ görbe alatti területét!

Megoldás

A tételben szereplõ

$a=1$ . Meg kell tehát állapítanunk a

$g(x)$ függvény

$1$ -ben eltûnõ integrálfüggvényét:

$\int g(x)\mbox{ d}x = \int x^2\mbox{ d}x = \frac{x^3}3 + c$ Ha azt akarjuk, hogy az

$x=1$ -ben a függvény eltûnjön, a

$c$ -t 'ügyesen'

$-\frac13$ -nak kell választani:

$\int\limits_1 x^2\mbox{ d}x = \frac{x^3}3 - \frac13$ A tétel szerint ez a terület függvénye. Ennek az

$x=3$ -ban felvett értéke a keresett terület:

$T(3) = \frac{3^3}3-\frac13 = 9-\frac13 = \color{darkred}{\mathbf{\frac{26}3}}$
A kédéses terület:

$\mathbf{\frac{26}3}$ .

Ez így egy kicsit hosszadalmas.

Praktikusan a következõképp végezzük ezt el...

Elõször is egy jelölés! A kérdéses területet, vagyis a $g(x)$ függvény 1-ben eltûnõ integrálfüggvényének a 3 helyen felvett értékét így jelöljük:
$\int\limits_1^3 g(x)\mbox{ d}x$ és úgy olvassuk: 'integrál 1-tõl 3-ig g(x)'. A neve: határozott integrál.

Hogyan számolhatjuk ki egyszerûen?
$\int\limits_1^3 g(x)\mbox{ d}x = \int\limits_1^3 x^2\mbox{ d}x = \left[\frac{x^3}3\right]_1^3 = \frac{3^3}3-\frac{1^3}3 = 9-\frac13 = \color{darkred}{\mathbf{\frac{26}3}}$
Az történt, hogy nem törõdtünk azzal, hogy melyik integrálfüggvénnyel dolgozunk. Behelyettesítettük elõbb az integrál felsõ határát, majd az alsó határát, s kivontuk õket egymásbõl. (A felsõ határ helyettesítési értékébõl az alsóét.)

Ez azért mûködõképes, mert az integrálfüggvények csak egy additív konstansban különböznek. És ha ügyelünk arra, hogy mind a két helyettesítésnél ugyanazt az integrálfüggvényt használjuk, akkor bármennyi is a kívánatos konstans, az a kivonás miatt kiesik.

Ha tehát az egyébként elõírt (tétel szerinti) $\frac{x^3}3-\frac13$ helyett önkényesen az $\frac{x^3}3$ -at használjuk, az nem okoz bajt, mert a kivonás miatt a gond kiesik.

Definíció: Legyen

$f(x)$ valamely

$[a;b]$ intervallumon (vagy azon túl is) értelmezett folytonos függvény!

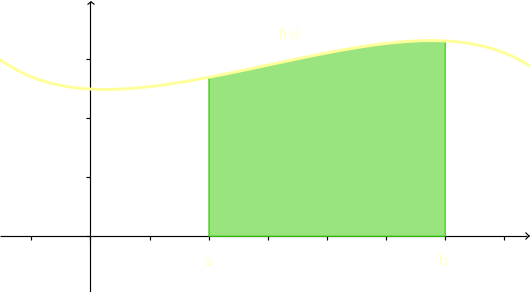
$\int\limits_a^b f(x)\mbox{ d}x$

olvasata:
'határozott integrál a-tól b-ig'

Jelentése:

$\int\limits_a^b f(x)\mbox{ d}x=F(b)-F(a)$ ahol

$F(x)$ az

$f(x)$ egyik primitív függvénye. (Mindegy melyik, mert a határozatlan

$c$ additív konstans a kivonás miatt úgyis kiesik.)

(A határozott integrál jelenti egyben a függvény grafikonja és az x-tengely közé esõ elõjeles terület nagyságát az [a;b] intervallumon.)

1. Megjegyzés: Az elmondás érthetõsége kedvéért azt feltételeztük, hogy a ≤ b. (Másképp [a;b] intervallum üres.) De a határozott integrál definícióját igazából nem zavarná, ha a > b lenne, akkor is

$F(b)-F(a)$ .
Ezt úgy fejezzük ki, hogy: a határozott integrál értéke elõjelet vált, ha a határokat felcseréljük:

$\int\limits_a^b f(x)\mbox{ d}x = -\int\limits_b^a f(x)\mbox{ d}x$
2. Megjegyzés: Nem minden függvénynek van primitív függvénye, nem minden halmaznak van területe, nem minden függvény integrálható, stb. Szóval mindezekhez hozzá kéne tenni: 'ha a primitív függvény létetik', 'ha az a terület létezik', 'ha a függvény integrálható', stb. De ezt középiskolában elhagyjuk. A mi függvényeink szépek, a mi halmazainknak van területük, ... persze néha nem. Nem árt az óvatosság!

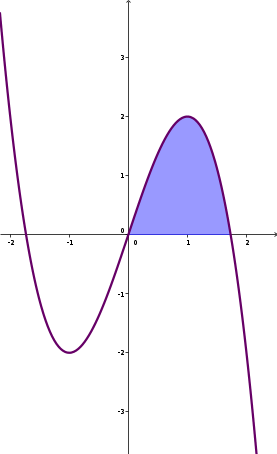
2. példa

Határozzuk meg a

$h(x)=3x-x^3$ függvény görbéjének az x-tengely pozitív felével közbezárt területét!

Megoldás

Az integrálás határai a

$h(x)$ fv. nemnegatív zérushelyei:

$0$ és

$\sqrt{3}$ .

Alkalmazzuk az új jelölést!

$\begin{equation} \begin{split} \int\limits_0^{\sqrt{3}} \left( 3x-x^3\right)\mbox{d}x &= \left[\frac32x^2-\frac14x^4\right]_0^{\sqrt{3}} = \left(\frac32\left(\sqrt{3}\right)^2-\frac14\left(\sqrt{3}\right)^4\right)-\\\\ &- \left(\frac32 0^2-\frac14 0^4\right) = \left(\frac92-\frac94\right)-0 = \color{darkred}{\mathbf{\frac94}} \end{split} \end{equation}$
A kédéses terület:

$\mathbf{\frac{9}4}$ .