
A koszinusz-függvény kiterjesztett értelmezése
Hegyesszög koszinusza
|
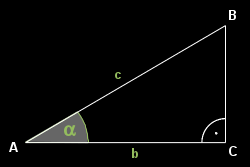 |
Hegyesszög koszinuszának értelmezése a koordináta-rendszerben...
| Ha a koordináta-rendszerben tekintünk
egy α hegyesszöget mint irányszög és az α
irányszögû egységvektort (1-hosszú vektor), ...
... akkor \(\cos\alpha\) jelentése: az \(\alpha\) irányszögû egységvektor elsõ koordinátája. Magyarázat: (1) Jelölje vektorunk elsõ koordinátáját x. (2) Az ábrán kiemelt derékszögû háromszögben felírva \(\cos\alpha\) értelmezését: |
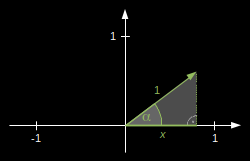 |
\[\cos\alpha = \frac{x}{1} =x\]
A koszinusz értelmezése
tetszõleges irányszögre
Ez a definíció tetszõleges \(\alpha\in\mathbb R\) elõjeles irányszög esetén értelmezi \(\alpha\) koszinuszát. Más szavakkal, értelmeztünk egy valós függvényt (neve: koszinusz-függvény): \[\cos: \mathbb R \longrightarrow \mathbb R\]
A koszinusz-függvény kirajzolása
A "kellemesebb" grafikon érdekében a szöget radiánban mérjük.
Miközben a szög növekszik a megfelelõ egységvektor elsõ koordinátája
más- és más értéket vesz fel. Ezt illusztrálja a következõ animáció:
(Az x-tengelyen a szög értéke
fut radiánban.)
A teljes grafikon jó átláthatósága érdekében az x-tengelyen a \(\pi\) többszöröseivel jelöljük a skálát.
A
koszinusz-függvény tulajdonságai
- Értelmezési tartomány: \(D_{\cos} = \mathbb R\) (Minden forgásszögnek van koszinusza.)
- Értékkészlet: \(R_{\cos} = [-1;1]\)
- Szélsõérték:
- Maximum
- értéke: \(y=1\)
- helye(i): \(x=k\cdot 2\pi\), \(k\in\mathbb Z\)
- Minimum
- értéke: \(y=-1\)
- helye(i): \(x=\pi+k\cdot 2\pi\), \(k\in\mathbb Z\)
- Zérushely(ei): \(x=\frac{\pi}{2}+k\cdot\pi\), \(k\in\mathbb Z\)
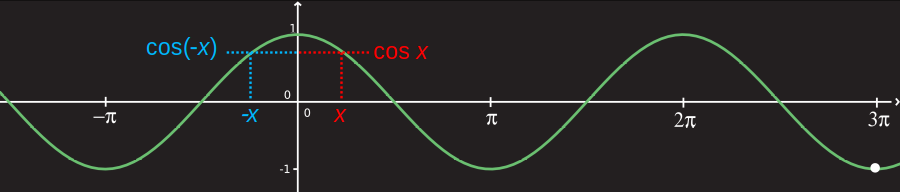
- Paritás: a függvény páros.
- Geometriai értelemben: a függvény grafikonja az y-tengelyre tengelyesen szimmetrikus.
- Algebrai értelemben: ha a fv. valamely \(x\) helyen a \(\cos x\) értéket veszi fel, akkor a \(-x\) helyen ugyanazt, azaz \(\cos(-x)=\cos x\).
- A függvény \(2\pi\) szerint periodikus.
- Geometriai értelemben: a fv. grafikonja \(2\pi\) vel eltolva az x tengely pozitív, vagy negatív irányába önmagába megy át
- Algebrai értelemben: \(\cos x = \cos(x+2\pi) = \cos(x-2\pi)\).